题目内容
函数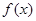 的定义域为
的定义域为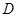 ,若存在闭区间[m,n]
,若存在闭区间[m,n] 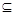 D,使得函数
D,使得函数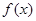 满足:①
满足:①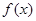
在[m,n]上是单调函数;②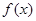 在[m,n]上的值域为[2m,2n],则称区间[m,n]为
在[m,n]上的值域为[2m,2n],则称区间[m,n]为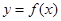 的
的
“倍值区间”.下列函数中存在“倍值区间”的有 (填上所有正确的序号)
①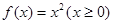 ; ②
; ②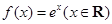 ;
;
③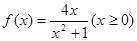 ; ④
; ④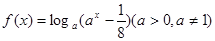
 的定义域为
的定义域为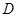 ,若存在闭区间[m,n]
,若存在闭区间[m,n] 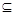 D,使得函数
D,使得函数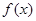 满足:①
满足:①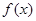
在[m,n]上是单调函数;②
 在[m,n]上的值域为[2m,2n],则称区间[m,n]为
在[m,n]上的值域为[2m,2n],则称区间[m,n]为 的
的“倍值区间”.下列函数中存在“倍值区间”的有 (填上所有正确的序号)
①
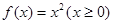 ; ②
; ②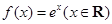 ;
;③
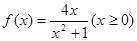 ; ④
; ④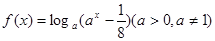
①③④.
解:函数中存在“倍值区间”,则:①f(x)在[a,b]内是单调函数;②
f(a)="2a," f(b)=2b或f(a)="2b," f(b)=2a
①f(x)=x2(x≥0),若存在“倍值区间”[a,b],则
A=0,b=2
∴f(x)=x2(x≥0),若存在“倍值区间”[0,2];
②f(x)=ex(x∈R),若存在“倍值区间”[a,b],则f(a)="2a," f(b)=2b
构建函数g(x)=ex-x,∴g′(x)=ex-1,∴函数在(-∞,0)上单调减,在(0,+∞)上单调增,∴函数在x=0处取得极小值,且为最小值.∵g(0)=1,∴,g(x)>0,∴ex-x=0无解,故函数不存在“倍值区间”;
③f(x)=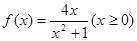
若存在“倍值区间”[a,b]⊆[0,1],则f(a)="2a," f(b)=2b
∴a=0,b=1,若存在“倍值区间”[0,1];
④f(x)=loga(ax-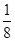 ),loga(am-)=2m,loga(an-
),loga(am-)=2m,loga(an-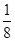 )="2n" (a>0,a≠1).不妨设a>1,则函数在定义域内为单调增函数
)="2n" (a>0,a≠1).不妨设a>1,则函数在定义域内为单调增函数
若存在“倍值区间”[m,n],则loga(an-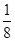 )=2n,loga(am-)=2m
)=2n,loga(am-)=2m
∴2m,2n是方程loga(ax-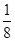 )=2x的两个根,∴2m,2n是方程a2x-ax+
)=2x的两个根,∴2m,2n是方程a2x-ax+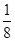 =0的两个根,由于该方程有两个不等的正根,故存在“倍值区间”[m,n];综上知,所给函数中存在“倍值区间”的有①③④
=0的两个根,由于该方程有两个不等的正根,故存在“倍值区间”[m,n];综上知,所给函数中存在“倍值区间”的有①③④
故选C.
f(a)="2a," f(b)=2b或f(a)="2b," f(b)=2a
①f(x)=x2(x≥0),若存在“倍值区间”[a,b],则
A=0,b=2
∴f(x)=x2(x≥0),若存在“倍值区间”[0,2];
②f(x)=ex(x∈R),若存在“倍值区间”[a,b],则f(a)="2a," f(b)=2b
构建函数g(x)=ex-x,∴g′(x)=ex-1,∴函数在(-∞,0)上单调减,在(0,+∞)上单调增,∴函数在x=0处取得极小值,且为最小值.∵g(0)=1,∴,g(x)>0,∴ex-x=0无解,故函数不存在“倍值区间”;
③f(x)=
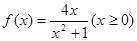
若存在“倍值区间”[a,b]⊆[0,1],则f(a)="2a," f(b)=2b
∴a=0,b=1,若存在“倍值区间”[0,1];
④f(x)=loga(ax-
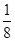 ),loga(am-)=2m,loga(an-
),loga(am-)=2m,loga(an-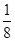 )="2n" (a>0,a≠1).不妨设a>1,则函数在定义域内为单调增函数
)="2n" (a>0,a≠1).不妨设a>1,则函数在定义域内为单调增函数若存在“倍值区间”[m,n],则loga(an-
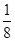 )=2n,loga(am-)=2m
)=2n,loga(am-)=2m∴2m,2n是方程loga(ax-
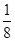 )=2x的两个根,∴2m,2n是方程a2x-ax+
)=2x的两个根,∴2m,2n是方程a2x-ax+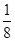 =0的两个根,由于该方程有两个不等的正根,故存在“倍值区间”[m,n];综上知,所给函数中存在“倍值区间”的有①③④
=0的两个根,由于该方程有两个不等的正根,故存在“倍值区间”[m,n];综上知,所给函数中存在“倍值区间”的有①③④故选C.

练习册系列答案
相关题目
 的定义域为
的定义域为 ,若所有点
,若所有点
 构成一个正方形区域,则
构成一个正方形区域,则 的值为( )
的值为( )



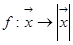 下,2的一个原像可以是( )
下,2的一个原像可以是( ) 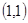
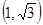

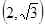
 满足
满足 ,
, 满足
满足 ,则
,则 等于( )
等于( ) ,则f(
,则f( )的解析式为____________
)的解析式为____________