题目内容
【题目】已知各项均为正数的无穷数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() (其中
(其中![]() 为常数),
为常数),![]()
![]() .数列
.数列![]() 满足
满足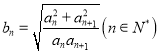 .
.
(1)证明数列![]() 是等差数列,并求出
是等差数列,并求出![]() 的通项公式;
的通项公式;
(2)若无穷等比数列![]() 满足:对任意的
满足:对任意的![]() ,数列
,数列![]() 中总存在两个不同的项
中总存在两个不同的项![]() ,
, ![]()
![]() 使得
使得![]() ,求
,求![]() 的公比
的公比![]() .
.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)仿写式子,两式相减得到![]() ,利用等差数列的定义和通项公式进行求解;(2)构造数列,利用递减数列得到取值范围,利用数列是特殊的函数,利用导数研究其单调性,利用
,利用等差数列的定义和通项公式进行求解;(2)构造数列,利用递减数列得到取值范围,利用数列是特殊的函数,利用导数研究其单调性,利用![]() 确定公比的取值.
确定公比的取值.
试题解析:(1)方法一:因为![]() ①,
①,
所以![]() ②,
②,
由②-①得, ![]()
![]() ,
,
即![]()
![]() ,又
,又![]() ,
,
则![]() ,即
,即![]() .
.
在![]() 中令
中令![]() 得,
得, ![]() ,即
,即![]() .
.
综上,对任意![]() ,都有
,都有![]() ,
,
故数列![]() 是以
是以![]() 为公差的等差数列.
为公差的等差数列.
又![]() ,则
,则![]() .
.
方法二:因为![]() ,所以
,所以![]() ,又
,又![]() ,
,
则数列![]() 是以
是以![]() 为首项,
为首项, ![]() 为公差的等差数列,
为公差的等差数列,
因此![]() ,即
,即![]() .
.
当![]() 时,
时, ![]() ,又
,又![]() 也符合上式,
也符合上式,
故![]() .
.
故对任意![]() ,都有
,都有![]() ,即数列
,即数列![]() 是以
是以![]() 为公差的等差数列.
为公差的等差数列.
(2)令![]() ,则数列
,则数列![]() 是递减数列,所以
是递减数列,所以![]() .
.
考察函数![]() ,因为
,因为![]() ,所以
,所以![]() 在
在![]() 上递增,因此
上递增,因此![]() ,从而
,从而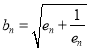
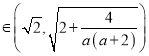 .
.
因为对任意![]() ,总存在数列
,总存在数列![]() 中的两个不同项
中的两个不同项![]() ,
, ![]() ,使得
,使得![]() ,所以对任意的
,所以对任意的![]() 都有
都有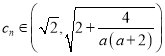 ,明显
,明显![]() .
.
若![]() ,当
,当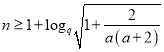 时,
时,
有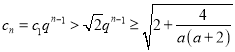 ,不符合题意,舍去;
,不符合题意,舍去;
若![]() ,当
,当![]() 时,
时,
有![]()
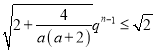 ,不符合题意,舍去;
,不符合题意,舍去;
故![]() .
.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
