题目内容
“不等式x2-x+m＞0在R上恒成立”的一个必要不充分条件是（ ）A．m
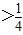
B．0＜m＜1
C．m＞0
D．m＞1
【答案】分析：根据“不等式x2-x+m＞0在R上恒成立”，令f（x）=x2-x+m，开口向上，根据判别式△＜0，求出m的范围，根据充分必要条件的定义，进行求解；
解答：解：∵“不等式x2-x+m＞0在R上恒成立”，
∴△=（-1）2-4m＜0，解得m＞
，
A、A是充要条件，故A错误；
B、因为m＞
推不出0＜m＜1，故B错误；
C、∵m＞
⇒m＞0，反之不能推出，故C正确；
D、∵m＞1⇒m＞
，所以m＞1是“不等式x2-x+m＞0在R上恒成立”的充分不必要条件，故D错误；
故选C；
点评：本题考查充分、必要条件的判断，涉及一元二次不等式的解法，解题的关键要掌握充分、必要条件定义．
解答：解：∵“不等式x2-x+m＞0在R上恒成立”，
∴△=（-1）2-4m＜0，解得m＞
，A、A是充要条件，故A错误；
B、因为m＞
推不出0＜m＜1，故B错误；C、∵m＞
⇒m＞0，反之不能推出，故C正确；D、∵m＞1⇒m＞
，所以m＞1是“不等式x2-x+m＞0在R上恒成立”的充分不必要条件，故D错误；故选C；
点评：本题考查充分、必要条件的判断，涉及一元二次不等式的解法，解题的关键要掌握充分、必要条件定义．
练习册系列答案
相关题目
命题p：若不等式x2+x+m＞0恒成立，则m＞
，命题q：在△ABC中，A＞B是sinA＞sinB的充要条件，则（ ）
| 1 |
| 4 |
| A、p真q假 |
| B、“p∧q”为真 |
| C、“p∨q”为假 |
| D、“?p∨?q”为真 |