题目内容
若不等式x2+x-m＞0的解集为{x|x＜-3或x＞2}，则m=
6
6
．分析：由不等式x2+x-m＞0的解集为{x|x＜-3或x＞2}，知-3和2是方程x2+x-m=0的两个实根，由此利用韦达定理能求出m．
解答：解：∵不等式x2+x-m＞0的解集为{x|x＜-3或x＞2}，
∴-3和2是方程x2+x-m=0的两个实根，
∴-3×2=-m，解得m=6．
故答案为：6．
∴-3和2是方程x2+x-m=0的两个实根，
∴-3×2=-m，解得m=6．
故答案为：6．
点评：本题考查一元二次不等式的应用，解题时要认真审题，仔细解答，注意韦达定理的合理运用．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
命题p：若不等式x2+x+m＞0恒成立，则m＞
，命题q：在△ABC中，A＞B是sinA＞sinB的充要条件，则（ ）
| 1 |
| 4 |
| A、p真q假 |
| B、“p∧q”为真 |
| C、“p∨q”为假 |
| D、“?p∨?q”为真 |
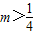，命题q：在△ABC中，A＞B是sinA＞sinB的充要条件，则（ ）