题目内容
已知,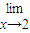
 =a,且函数y=alnx+
=a,且函数y=alnx+ +c在(1,e)上具有单调性,则b的取值范围是( )
+c在(1,e)上具有单调性,则b的取值范围是( )A.(-∞,1]∪[e,+∞]
B.(-∞,0]∪[e,+∞]
C.(-∞,e]
D.[1,e]
【答案】分析:先由
 =a,求得a=1,c=-3,从而得到y=alnx+
=a,求得a=1,c=-3,从而得到y=alnx+ +c=
+c= ,再由“函数y=alnx+
,再由“函数y=alnx+ +c在(1,e)上具有单调性”转化为“
+c在(1,e)上具有单调性”转化为“ 或
或 在(1,e)上恒成立”,再令t=
在(1,e)上恒成立”,再令t= ∈(
∈( )转化为-bt2+t≥0或-bt2+t≤0在(
)转化为-bt2+t≥0或-bt2+t≤0在( )上恒成立,由二次函数的性质求解.
)上恒成立,由二次函数的性质求解.
解答:解:∵
 =a,
=a,
∴a=1,c=-3,
∴y=alnx+ +c=
+c=
∵函数y=alnx+ +c在(1,e)上具有单调性
+c在(1,e)上具有单调性
∴ 或
或 在(1,e)上恒成立
在(1,e)上恒成立
∴令t= ∈(
∈( )
)
∴-bt2+t≥0或-bt2+t≤0
∴b≤1或b≥e
故选A
点评:本题主要考查导数法研究函数的单调性,基本思路:当函数是增函数时,导数大于等于零恒成立,当函数是减函数时,导数小于等于零恒成立,然后转化为求相应函数的最值问题.

 =a,求得a=1,c=-3,从而得到y=alnx+
=a,求得a=1,c=-3,从而得到y=alnx+ +c=
+c= ,再由“函数y=alnx+
,再由“函数y=alnx+ +c在(1,e)上具有单调性”转化为“
+c在(1,e)上具有单调性”转化为“ 或
或 在(1,e)上恒成立”,再令t=
在(1,e)上恒成立”,再令t= ∈(
∈( )转化为-bt2+t≥0或-bt2+t≤0在(
)转化为-bt2+t≥0或-bt2+t≤0在( )上恒成立,由二次函数的性质求解.
)上恒成立,由二次函数的性质求解.解答:解:∵

 =a,
=a,∴a=1,c=-3,
∴y=alnx+
 +c=
+c=
∵函数y=alnx+
 +c在(1,e)上具有单调性
+c在(1,e)上具有单调性∴
 或
或 在(1,e)上恒成立
在(1,e)上恒成立∴令t=
 ∈(
∈( )
)∴-bt2+t≥0或-bt2+t≤0
∴b≤1或b≥e
故选A
点评:本题主要考查导数法研究函数的单调性,基本思路:当函数是增函数时,导数大于等于零恒成立,当函数是减函数时,导数小于等于零恒成立,然后转化为求相应函数的最值问题.

练习册系列答案
相关题目
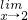
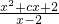 =a,且函数y=alnx+
=a,且函数y=alnx+ +c在(1,e)上具有单调性,则b的取值范围是
+c在(1,e)上具有单调性,则b的取值范围是
 =a,且函数y=alnx+
=a,且函数y=alnx+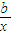 +c在(1,e)上具有单调性,则b的取值范围是( )
+c在(1,e)上具有单调性,则b的取值范围是( )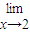
 =a,且函数y=alnx+
=a,且函数y=alnx+ +c在(1,e)上具有单调性,则b的取值范围是( )
+c在(1,e)上具有单调性,则b的取值范围是( )
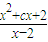 =a,且函数y=alnx+
=a,且函数y=alnx+ +c在(1,e)上具有单调性,则b的取值范围是( )
+c在(1,e)上具有单调性,则b的取值范围是( )