题目内容
3.以下三个命题:①?c∈R,c2≥c;②?a∈R,使y=x2+ax+1为偶函数;③x∈(1,2),(a2+1)x+2>0.正确命题的序号为②③(写出所有正确命题的序号).分析 举出反例c=$\frac{1}{2}$,可判断①;举出正例a=0,可判断②;根据一次函数的图象和性质,可判断③.
解答 解:①当c=$\frac{1}{2}$时,c2<c,故?c∈R,c2≥c错误;
②?a=0∈R,使y=x2+ax+1为偶函数,故正确;
③由a2+1≥1,可得y=(a2+1)x+2为增函数,
当x∈(1,2),(a2+1)x+2>a2+1+2≥3>0,故正确.
故正确的命题的序号为:②③,
故答案为:②③.
点评 本题考查的知识点是命题的真假判断与应用,此类题型往往综合较多的其它知识点,综合性强,难度中档.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
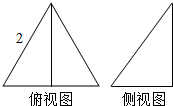 已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.
已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.