题目内容
过点(0,-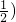 的直线l与抛物线y=-x2交于A、B两点,O为坐标原点,则
的直线l与抛物线y=-x2交于A、B两点,O为坐标原点,则 的值为
的值为
- A.

- B.

- C.-4
- D.无法确定
B
分析:法一:根据抛物线的标准方程,当AB的斜率为0时,可得A,B,求得 的值,结合选择题的特点,得出结论.
的值,结合选择题的特点,得出结论.
法二:由抛物线y=-x2与过其焦点(0,- )的直线方程联立,消去y整理成关于x的一元二次方程,设出A(x1,y1)、B(x2,y2)两点坐标,
)的直线方程联立,消去y整理成关于x的一元二次方程,设出A(x1,y1)、B(x2,y2)两点坐标,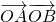 =x1•x2+y1•y2,由韦达定理可以求得答案.
=x1•x2+y1•y2,由韦达定理可以求得答案.
解答:法一:当AB的斜率K=0时,可得A(- ,-
,- ),B(
),B( 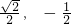 )
)
∴ =(
=( 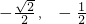 )•(
)•(  ,-
,- )=-
)=-
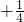 =
=
故选B
法二:,由题意可得直线AB的斜率存在
∴直线AB的方程为y=kx ,
,
由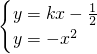 得
得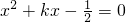 ,设A(x1,y1),B(x2,y2),
,设A(x1,y1),B(x2,y2),
则 x1+x2=-k,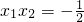
∴y1•y2=(kx1 )•(kx2
)•(kx2 )=k2x1•x2-
)=k2x1•x2- k(x1+x2)
k(x1+x2)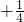 =
=
∴ =x1•x2+y1•y2=
=x1•x2+y1•y2=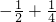 =
=
故选B
点评:本题考查抛物线的标准方程,以及简单性质的应用,两个向量的数量积公式,其中法一中,通过给变量取特殊值,检验所给的选项,是一种简单有效的方法,在此类对于参数K取任意值时所研究的对象取值不变的前提下,应用特殊值法解决此类问题最有效,最直接,注意此方法的应用的原理.
分析:法一:根据抛物线的标准方程,当AB的斜率为0时,可得A,B,求得
 的值,结合选择题的特点,得出结论.
的值,结合选择题的特点,得出结论.法二:由抛物线y=-x2与过其焦点(0,-
 )的直线方程联立,消去y整理成关于x的一元二次方程,设出A(x1,y1)、B(x2,y2)两点坐标,
)的直线方程联立,消去y整理成关于x的一元二次方程,设出A(x1,y1)、B(x2,y2)两点坐标,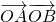 =x1•x2+y1•y2,由韦达定理可以求得答案.
=x1•x2+y1•y2,由韦达定理可以求得答案.解答:法一:当AB的斜率K=0时,可得A(-
 ,-
,- ),B(
),B( 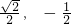 )
)∴
 =(
=( 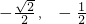 )•(
)•(  ,-
,- )=-
)=-
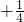 =
=
故选B
法二:,由题意可得直线AB的斜率存在
∴直线AB的方程为y=kx
 ,
,由
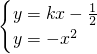 得
得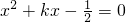 ,设A(x1,y1),B(x2,y2),
,设A(x1,y1),B(x2,y2),则 x1+x2=-k,
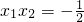
∴y1•y2=(kx1
 )•(kx2
)•(kx2 )=k2x1•x2-
)=k2x1•x2- k(x1+x2)
k(x1+x2)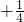 =
=
∴
 =x1•x2+y1•y2=
=x1•x2+y1•y2=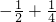 =
=
故选B
点评:本题考查抛物线的标准方程,以及简单性质的应用,两个向量的数量积公式,其中法一中,通过给变量取特殊值,检验所给的选项,是一种简单有效的方法,在此类对于参数K取任意值时所研究的对象取值不变的前提下,应用特殊值法解决此类问题最有效,最直接,注意此方法的应用的原理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
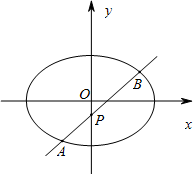 已知椭圆
已知椭圆