题目内容
把函数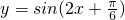 的图象向右平移
的图象向右平移 个单位后,所得图象的一条对称轴方程为
个单位后,所得图象的一条对称轴方程为
- A.
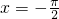
- B.
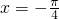
- C.

- D.

A
分析:函数y=f(x)图象向右平移 个单位,得f(x-
个单位,得f(x- )=
)= 的图象,由正弦曲线的对称性,得函数y=
的图象,由正弦曲线的对称性,得函数y= 图象的对称轴方程为:x=
图象的对称轴方程为:x= (k+1)π,k∈Z.最后取k=-2,得
(k+1)π,k∈Z.最后取k=-2,得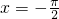 ,即得本题答案.
,即得本题答案.
解答:设f(x)=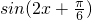 ,得图象向右平移
,得图象向右平移 个单位后,
个单位后,
得到的表达式为f(x- )=
)= =
=
对于函数y= ,令
,令 =
= ,得x=
,得x= (k+1)π,k∈Z
(k+1)π,k∈Z
∴函数y= 图象的对称轴方程为:x=
图象的对称轴方程为:x= (k+1)π,k∈Z
(k+1)π,k∈Z
取k=-2,得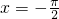 ,
,
故选:A
点评:本题将三角函数图象平移后,求所得图象的一条对称轴,着重考查了函数图象平移公式和正弦曲线的对称性等知识,属于基础题.
分析:函数y=f(x)图象向右平移
 个单位,得f(x-
个单位,得f(x- )=
)= 的图象,由正弦曲线的对称性,得函数y=
的图象,由正弦曲线的对称性,得函数y= 图象的对称轴方程为:x=
图象的对称轴方程为:x= (k+1)π,k∈Z.最后取k=-2,得
(k+1)π,k∈Z.最后取k=-2,得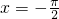 ,即得本题答案.
,即得本题答案.解答:设f(x)=
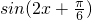 ,得图象向右平移
,得图象向右平移 个单位后,
个单位后,得到的表达式为f(x-
 )=
)= =
=
对于函数y=
 ,令
,令 =
= ,得x=
,得x= (k+1)π,k∈Z
(k+1)π,k∈Z∴函数y=
 图象的对称轴方程为:x=
图象的对称轴方程为:x= (k+1)π,k∈Z
(k+1)π,k∈Z取k=-2,得
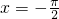 ,
,故选:A
点评:本题将三角函数图象平移后,求所得图象的一条对称轴,着重考查了函数图象平移公式和正弦曲线的对称性等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
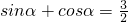 ;
;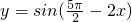 是偶函数;
是偶函数; 是函数
是函数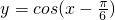 图象的一条对称轴方程;
图象的一条对称轴方程;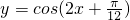 的图象向右平移
的图象向右平移 个单位,所得的函数解析式为
个单位,所得的函数解析式为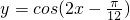
 的图象关于点
的图象关于点 对称;
对称; 的最小正周期是π;
的最小正周期是π; 的图象向右平移
的图象向右平移 个单位可得到y=2sin2x的图象.
个单位可得到y=2sin2x的图象.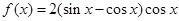 的四个结论:
的四个结论: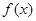 的最大值为
的最大值为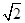 ;
;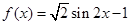 的图象向右平移
的图象向右平移 个单位后可得到函数
个单位后可得到函数 ],
],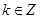 ;
; 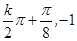 ),
),