题目内容
己知函数f(x)是定义在R上的偶函数,且对任意的x∈R,都有f(x+2)=f(x).当0≤x≤1对,f(x)=x2.若直线y=x+a与函数y=f(x)的图象在[0,2]内恰有两个不同的公共点,则实数a的值是
- A.0
- B.0或

- C.0或

- D.
 或
或
C
分析:由题意可得函数的图象,属性结合可得当直线为图中的m,或n是满足题意,求出其对应的a值即可.
解答:由对任意的x∈R,都有f(x+2)=f(x)可知,函数的周期为T=2,
结合函数为偶函数,且当0≤x≤1对,f(x)=x2可作出函数y=f(x)和直线y=x+a的图象,

当直线为图中的直线m,n时,满足题意,易知当直线为m时,过原点,a=0,
当直线为n时,直线与曲线相切,联立 ,消y可得x2-x-a=0,
,消y可得x2-x-a=0,
由△=1+4a=0可得a= ,故a的值为0,或
,故a的值为0,或 ,
,
故选C
点评:本题考查根的存在性与个数的判断,涉及函数的奇偶性与周期性,数形结合的思想,属中档题.
分析:由题意可得函数的图象,属性结合可得当直线为图中的m,或n是满足题意,求出其对应的a值即可.
解答:由对任意的x∈R,都有f(x+2)=f(x)可知,函数的周期为T=2,
结合函数为偶函数,且当0≤x≤1对,f(x)=x2可作出函数y=f(x)和直线y=x+a的图象,

当直线为图中的直线m,n时,满足题意,易知当直线为m时,过原点,a=0,
当直线为n时,直线与曲线相切,联立
 ,消y可得x2-x-a=0,
,消y可得x2-x-a=0,由△=1+4a=0可得a=
 ,故a的值为0,或
,故a的值为0,或 ,
,故选C
点评:本题考查根的存在性与个数的判断,涉及函数的奇偶性与周期性,数形结合的思想,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
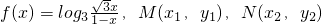 是f(x)图象点的两点,横坐标为
是f(x)图象点的两点,横坐标为 的点P是M,N的中点.
的点P是M,N的中点.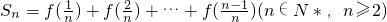 ,
,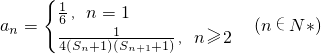 ,Tn为数列{an}前n项和,当Tn<m(Sn+1+1)对一切n∈N*都成立时,试求实数m的取值范围.
,Tn为数列{an}前n项和,当Tn<m(Sn+1+1)对一切n∈N*都成立时,试求实数m的取值范围.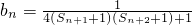 ,Bn为数列{bn}前n项和,证明:
,Bn为数列{bn}前n项和,证明: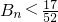 .
.