题目内容
已知点P是双曲线
上的动点，F1，F2分别是其左、右焦点，O为坐标原点，则
的取值范围（ ）A．（2，3）
B．（2，
]C．[2，3）
D．[2，
]
【答案】分析：设P（x，y） 则y2=
-4，e=
，由焦半径公式能够得出|PF1|=ex+a，|PF2|=ex-a，代入所求的式子并化简得到 
，再由双曲线中x2≥8，求出范围即可．
解答：
解：设P（x，y） 根据双曲线的对称性，不妨设x＞0，
由焦半径公式|PF1|=ex+a，|PF2|=ex-a，
则
=
（y2=
-4，e=
），
则原式=
=
，又因为双曲线中x2≥8．
所以
∈（2，
]．
所以
的取值范围为（2，
]．
故选B．
点评：本题考查了双曲线的性质、函数的值域等基础知识，考查运算求解能力，考查归与转化思想，属于中档题．
-4，e=，由焦半径公式能够得出|PF1|=ex+a，|PF2|=ex-a，代入所求的式子并化简得到 ，再由双曲线中x2≥8，求出范围即可．解答：
解：设P（x，y） 根据双曲线的对称性，不妨设x＞0，由焦半径公式|PF1|=ex+a，|PF2|=ex-a，
则
= （y2=-4，e=），则原式=
=，又因为双曲线中x2≥8．所以
∈（2，]．所以
的取值范围为（2，]．故选B．
点评：本题考查了双曲线的性质、函数的值域等基础知识，考查运算求解能力，考查归与转化思想，属于中档题．
练习册系列答案
相关题目
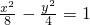上的动点，F1，F2分别是其左、右焦点，O为坐标原点，则
的取值范围
]
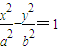上除顶点外的任意一点，F1、F2分别为左、右焦点，c为半焦距，△PF1F2的内切圆与F1F2切于点M，则|F1M|•|F2M|= ．
上的动点，F1、F2分别是其左、右焦点，O为坐标原点，
的取值范围 （ ）
B．
C．
D．
上的动点，F1、F2分别是其左、右焦点，O为坐标原点，
的取值范围 （ ）
B．
C．
D．