题目内容
（理）在平面内，已知P是定线段AB外一点，满足下列条件：
则△PAB的内切圆面积为
- A.
- B.
- C.
- D.
D
分析：根据条件先确定△PAB为直角三角形，然后根据
求出两直角边，根据公式r=
可求内切圆的半径（a，b，c，r分别为直角三角形的直角边及斜边，内切圆半径），进而可求面积
解答：∵P是定线段AB外一点且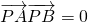
∴△PAB为直角三角形，且∠APB=90°
设
=m，
=n，
∵
∴m-n=2，
∴（m-n）2=m2+n2-2mn=20-2mn
∴mn=8
∴m=4，n=2
△PAB的内切圆的半径r=
=
=
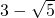
内切圆的面积为
故选D．
点评：本题主要考查了向量在几何中的应用，以及三角形面积的度量，同时考查转化的思想和计算能力，属于中档题．
分析：根据条件先确定△PAB为直角三角形，然后根据
求出两直角边，根据公式r=可求内切圆的半径（a，b，c，r分别为直角三角形的直角边及斜边，内切圆半径），进而可求面积解答：∵P是定线段AB外一点且
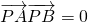
∴△PAB为直角三角形，且∠APB=90°
设
=m，=n，∵
∴m-n=2，
∴（m-n）2=m2+n2-2mn=20-2mn
∴mn=8
∴m=4，n=2
△PAB的内切圆的半径r=
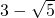
==内切圆的面积为
故选D．
点评：本题主要考查了向量在几何中的应用，以及三角形面积的度量，同时考查转化的思想和计算能力，属于中档题．
练习册系列答案
相关题目
的棱长为2，点
是正方形
的中心，点
、
分别是棱
的中点．设点
分别是点
内的正投影．
在平面
平面
；
所成角的正弦值.
满足：
（1）求函数
，求证：
；（3）若不等式
对任意
及任意
都成立，求实数
的取值范围。