题目内容
16.若关于x的方程$\frac{lnx}{x}$-a=0(e为自然对数的底数)有两个实数根,则实数a的取值范围是(-∞,$\frac{1}{e}$].分析 利用已知条件转化方程为lnx=ax,令y=lnx与y=ax的函数图象有交点即可得出a的范围.
解答 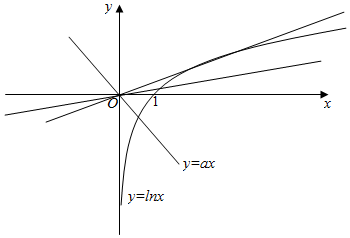 解:由$\frac{lnx}{x}$-a=0,得lnx=ax,
解:由$\frac{lnx}{x}$-a=0,得lnx=ax,
∴y=lnx与y=ax的函数图象有公共点,
作出y=lnx与y=ax的函数图象如图所示:
显然当a≤0时,y=ax与y=lnx的图象总有交点,符合题意;
设直线y=kx与y=lnx相切,切点为(x0,y0),
则$\left\{\begin{array}{l}{{y}_{0}=k{x}_{0}}\\{{y}_{0}=ln{x}_{0}}\\{\frac{1}{{x}_{0}}=k}\end{array}\right.$,解得k=$\frac{1}{e}$.
∴当0<a≤$\frac{1}{e}$时,y=ax与y=lnx的图象有交点,符合题意;
当a>$\frac{1}{e}$时,y=ax与y=lnx的图象没有交点,不符合题意.
综上,a的取值范围是(-∞,$\frac{1}{e}$],
故答案为:(-∞,$\frac{1}{e}$].
点评 本题考查了方程的根与函数图象的关系,开心数形结合思想的应用,属于中档题.

练习册系列答案
相关题目
6.已知sinα+sinβ+sinγ=0和cosα+cosβ+cosγ=0,则cos(α-β)的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
8.已知$\frac{a+i}{i}$=b+2i(a,b∈R),其中为虚数单位,则a-b=( )
| A. | -3 | B. | -2 | C. | -1 | D. | 1 |
6.对具有线性相关关系的变量x,y有一组观测数据(xi,yi)(i=1,2,…,8),其回归直线方程是$\hat y=\frac{1}{2}x+a$且x1+x2+…+x8=2,y1+y2+…+y8=5,则实数a是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |