题目内容
如图,四点A、B、C、D共圆,AC与BD相交于M, ,
, ,∠ADB=60°,∠CBD=15°,则AB的长为( )
,∠ADB=60°,∠CBD=15°,则AB的长为( )
A.

B.

C.

D.

【答案】分析:由已知中A、B、C、D四点共圆,由圆周角定理可得:∠ADB=∠ACB=60°,∠CBD=∠CAD=15°,进而∠BMA=∠CMD=75°,根据正弦定理,我们可以求出AM,CM的长,进而求出AC长,再由余弦定理,即可得到AB的长.
解答:解:由已知中,A、B、C、D四点共圆,
∴∠ADB=∠ACB=60°,∠CBD=∠CAD=15°,
∴∠BMA=75°,
由正弦定理可得,在△ABM中
AB=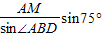
在△ABD中
AB=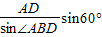
∴AM=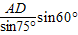 =
=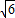
在△CBM中
CD=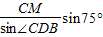
在△CBD中
CD=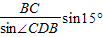
∴CM=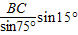 =2
=2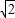
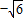
∴AC=2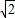
在△ABC中,AB=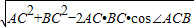 =
=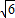
故选B
点评:本题考查的知识点是正弦定理和余弦定理,是平面几何三角形问题的综合应用,除解三角形外,根据四点共圆及圆周角定理得到:∠ADB=∠ACB,∠CBD=∠CAD,根据三角形外角和定理求出∠BMA=∠CMD=75°,都是解答的关键,难度较大.
解答:解:由已知中,A、B、C、D四点共圆,
∴∠ADB=∠ACB=60°,∠CBD=∠CAD=15°,
∴∠BMA=75°,
由正弦定理可得,在△ABM中
AB=
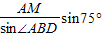
在△ABD中
AB=
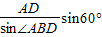
∴AM=
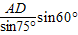 =
=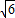
在△CBM中
CD=
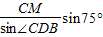
在△CBD中
CD=
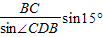
∴CM=
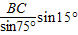 =2
=2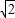
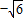
∴AC=2
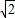
在△ABC中,AB=
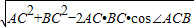 =
=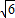
故选B
点评:本题考查的知识点是正弦定理和余弦定理,是平面几何三角形问题的综合应用,除解三角形外,根据四点共圆及圆周角定理得到:∠ADB=∠ACB,∠CBD=∠CAD,根据三角形外角和定理求出∠BMA=∠CMD=75°,都是解答的关键,难度较大.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目


 ,
, ,∠ADB=60°,∠CBD=15°,则AB的长为( )
,∠ADB=60°,∠CBD=15°,则AB的长为( )




 ,AD=1+
,AD=1+ ,∠ADB=60°,∠CBD=15°,则AB的长为
,∠ADB=60°,∠CBD=15°,则AB的长为 


 +
+
