题目内容
若f（x）是偶函数，且f（x）在区间[0，+∞）上是单调增函数，且f（-2）=0，则不等式（x-2）f（x-1）＞0的解集是 ．
分析：由已知判断出f（x）的单调性及图象上的特殊点，作出函数的草图，根据图象可解不等式．
解答：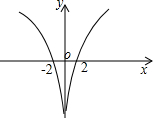
解：∵f（x）是偶函数，且f（x）在[0，+∞）上是增函数，
∴f（x）在（-∞，0]上是减函数，
由f（-2）=0，得f（2）=0，
作出f（x）的草图，如图所示：
由图象，得（x-2）f（x-1）＞0?
或
?
或
，
解得x＞3或-1＜x＜2，
∴（x-2）f（x-1）＞0的解集为：（3，+∞）∪（-1，2），
故答案为：（3，+∞）∪（-1，2）．
解：∵f（x）是偶函数，且f（x）在[0，+∞）上是增函数，∴f（x）在（-∞，0]上是减函数，
由f（-2）=0，得f（2）=0，
作出f（x）的草图，如图所示：
由图象，得（x-2）f（x-1）＞0?
|
|
|
|
解得x＞3或-1＜x＜2，
∴（x-2）f（x-1）＞0的解集为：（3，+∞）∪（-1，2），
故答案为：（3，+∞）∪（-1，2）．
点评：本题考查函数的奇偶性、单调性的综合应用，考查不等式的解法，考查数形结合思想，解决本题的关键是利用函数性质作出草图．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目