题目内容
如图,在正方体ABCD-A1B1C1D1中,E是棱A1D1的中点,H为平面EDB
内一点,
=(2m,-2m,-m)(m<0).
(1)证明HC1⊥平面EDB;
(2)求BC1与平面EDB所成的角;
(3)若正方体的棱长为a,求三棱锥A-EDB的体积.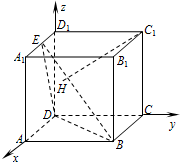
内一点,
| HC1 |
(1)证明HC1⊥平面EDB;
(2)求BC1与平面EDB所成的角;
(3)若正方体的棱长为a,求三棱锥A-EDB的体积.

证明:(1)设正方体的棱长为a,则
={
, 0 , a },
={ a , a , 0 }
∵
•
=0 ,
•
=0
∴
⊥
,
⊥
又∵DE∩DB=D
∴HC1⊥平面EDB.
(2)
={ -a ,0 , a },设
与
所成的角为θ
∵cosθ=
=
=
∴θ=45°.
由(1)知HC1⊥平面EDB
∴∠C1BH为BC1与平面EDB所成的角
∴∠C1BH=90°-45°=45°
(3)VA-EDB=VE-ABD=
•
a2•a=
a3.
| DE |
| a |
| 2 |
| DB |
∵
| HC1 |
| DE |
| HC1 |
| DB |
∴
| HC1 |
| DE |
| HC1 |
| DB |
又∵DE∩DB=D
∴HC1⊥平面EDB.
(2)
| BC1 |
| BC1 |
| HC1 |
∵cosθ=
| ||||
|
|
| 2ma+ma | ||
|
| ||
| 2 |
∴θ=45°.
由(1)知HC1⊥平面EDB
∴∠C1BH为BC1与平面EDB所成的角
∴∠C1BH=90°-45°=45°
(3)VA-EDB=VE-ABD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |

练习册系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )