题目内容
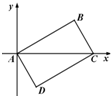
如图,在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标:A(0,0),B(3,
),C(4,0).
(1)求边CD所在直线的方程(结果写成一般式);
(2)证明平行四边形ABCD为矩形,并求其面积.
| 3 |
(1)求边CD所在直线的方程(结果写成一般式);
(2)证明平行四边形ABCD为矩形,并求其面积.

由于平行四边形ABCD的三个顶点坐标:A(0,0),B(3,
),C(4,0).
则kAB=
=
,kBC=
=-
,
(1)由于AB∥CD,则直线CD的方程为:y-0=
(x-4),
即边CD所在直线的方程为:x-
y-4=0;
(2)由于kAB=
=
,
kBC=
=-
,
则直线AB与BC的斜率之积为-1,即AB⊥BC,
故平行四边形ABCD为矩形,
又由AB=
=2
,BC=
=2,
则矩形ABCD的面积为4
.
| 3 |
则kAB=
| ||
| 3-0 |
| ||
| 3 |
| ||
| 3-4 |
| 3 |
(1)由于AB∥CD,则直线CD的方程为:y-0=
| ||
| 3 |
即边CD所在直线的方程为:x-
| 3 |
(2)由于kAB=
| ||
| 3-0 |
| ||
| 3 |
kBC=
| ||
| 3-4 |
| 3 |
则直线AB与BC的斜率之积为-1,即AB⊥BC,
故平行四边形ABCD为矩形,
又由AB=
| 3+32 |
| 3 |
| 1+3 |
则矩形ABCD的面积为4
| 3 |

练习册系列答案
相关题目