题目内容
函数y=log2(6+x-2x2)的一个单调递减区间是
- A.(2,+∞)
- B.
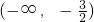
- C.
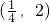
- D.

C
分析:先求原函数的定义域,再将原函数分解成两个简单函数y=log2z、z=6+x-2x2,因为y=log2z单调递增,所以要求原函数的单调递减区间即要求z=6+x-2x2的减区间(根据同增异减的性质),再由定义域即可得到答案.
解答:∵函数y=log2(6+x-2x2有意义∴6+x-2x2>0?(x-2)(2x+3)<0? <x<2
<x<2
∵2>1∴函数y=log2(6+x-2x2)的单调递减区间就是g(x)=6+x-2x^2的单调递减区间.
对于y=g(x)=6+x-2x2,开口向下,对称轴为x= ,
,
∴g(x)=6+x-2x2的单调递减区间是( ,+∞).
,+∞).
∵ <x<2,∴函数y=log2(6+x-2x2)的单调递减区间是(1/4,2)
<x<2,∴函数y=log2(6+x-2x2)的单调递减区间是(1/4,2)
故选C.
点评:本题主要考查复合函数单调性的问题.求复合函数单调性时注意同增异减的性质即可.
分析:先求原函数的定义域,再将原函数分解成两个简单函数y=log2z、z=6+x-2x2,因为y=log2z单调递增,所以要求原函数的单调递减区间即要求z=6+x-2x2的减区间(根据同增异减的性质),再由定义域即可得到答案.
解答:∵函数y=log2(6+x-2x2有意义∴6+x-2x2>0?(x-2)(2x+3)<0?
 <x<2
<x<2∵2>1∴函数y=log2(6+x-2x2)的单调递减区间就是g(x)=6+x-2x^2的单调递减区间.
对于y=g(x)=6+x-2x2,开口向下,对称轴为x=
 ,
,∴g(x)=6+x-2x2的单调递减区间是(
 ,+∞).
,+∞).∵
 <x<2,∴函数y=log2(6+x-2x2)的单调递减区间是(1/4,2)
<x<2,∴函数y=log2(6+x-2x2)的单调递减区间是(1/4,2)故选C.
点评:本题主要考查复合函数单调性的问题.求复合函数单调性时注意同增异减的性质即可.

练习册系列答案
相关题目
函数y=log2(6+x-2x2)的一个单调递减区间是( )
| A、(2,+∞) | ||||
B、(-∞,-
| ||||
C、(
| ||||
D、(-
|
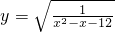 的定义域为B (1)求集合A与B;(2)求A∩B、(CUA)∪B
的定义域为B (1)求集合A与B;(2)求A∩B、(CUA)∪B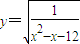 的定义域为B (1)求集合A与B;(2)求A∩B、(CUA)∪B
的定义域为B (1)求集合A与B;(2)求A∩B、(CUA)∪B