题目内容
9.已知双曲线M:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的一个焦点到一条渐近线的距离为$\frac{{\sqrt{2}}}{3}c$(c为双曲线的半焦距长),则双曲线的离心率e为( )| A. | $\frac{{\sqrt{7}}}{3}$ | B. | $\frac{{3\sqrt{7}}}{2}$ | C. | $\frac{{3\sqrt{7}}}{7}$ | D. | $3\sqrt{7}$ |
分析 根据双曲线方程可得它的渐近线方程为bx±ay=0,焦点坐标为(±c,0).利用点到直线的距离,结合已知条件列式,可得b,c关系,利用双曲线离心率的公式,可以计算出该双曲线的离心率.
解答 解:双曲线双曲线M:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的渐近线方程为bx±ay=0,焦点坐标为(±c,0),其中c=$\sqrt{{a}^{2}+{b}^{2}}$
∴一个焦点到一条渐近线的距离为d=$\frac{|±bc|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{{\sqrt{2}}}{3}c$,即7b2=2a2,
由此可得双曲线的离心率为e=$\frac{c}{a}$=$\frac{3\sqrt{7}}{7}$.
故选:C.
点评 本题给出双曲线一个焦点到渐近线的距离与焦距的关系,求双曲线的离心率,着重考查了双曲线的标准方程和简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
17.4名同学参加3项不同的课外活动,若每名同学可自由选择参加其中的一项,则每项活动至少有一名同学参加的概率为( )
| A. | $\frac{4}{9}$ | B. | $\frac{4}{27}$ | C. | $\frac{9}{64}$ | D. | $\frac{3}{64}$ |
4.复数$\frac{1-i}{1-2i}$的虚部为( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{3}{5}$ |
14.已知点(x,y)满足不等式组$\left\{\begin{array}{l}{x-4y+3≤0}\\{2x-y-1≥0}\\{3x+2y-19≤0}\end{array}\right.$,则z=x-2y的最大值为( )
| A. | -7 | B. | -1 | C. | 1 | D. | 2 |
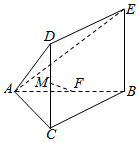 在如图所示的空间几何体中,AC⊥BC,四边形DCBE为矩形,点F,M分别为AB,CD的中点.
在如图所示的空间几何体中,AC⊥BC,四边形DCBE为矩形,点F,M分别为AB,CD的中点.