题目内容
【题目】已知数列![]() 满足
满足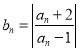 ,其中
,其中![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
(B)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)设![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(A)(1)详见解析;(2)详见解析. (B)(1)详见解析;(2)![]() .
.
【解析】试题分析:(A)(1)利用![]() 的递推关系得到
的递推关系得到![]() ,从而求得
,从而求得![]() ,由此猜想
,由此猜想![]() .(2)将
.(2)将![]() 的表达式代入
的表达式代入![]() ,求得
,求得![]() ,用裂项求和法求得前
,用裂项求和法求得前![]() 项和
项和![]() .(B)利用
.(B)利用![]() ,和
,和![]() 的递推关系,可求得
的递推关系,可求得![]() 的值,由此猜想
的值,由此猜想![]() .(2)利用
.(2)利用![]() ,可求得
,可求得![]() 的通项公式,代入
的通项公式,代入![]() 并化简,利用基本不等式可求得其最大值.
并化简,利用基本不等式可求得其最大值.
试题解析:
(A)解(1)由题意, ![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
,
猜想得: ![]() .
.
(2)由(1)得![]() ,
,
则![]()
![]() .
.
(B)解(1)![]() ,
,
由![]() ,得
,得![]() ,
,
同理可得![]() ,
, ![]() ,
,
猜想: ![]() .
.
(2)由(1),![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() 满足止式,
满足止式,
所以![]() ,
,
则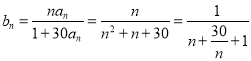 ,
, ![]() ,
,
设![]() ,则有
,则有![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
因为![]() ,且
,且![]() ,
,
所以当![]() 或
或![]() 时,
时, ![]() 有最大值
有最大值![]() .
.

练习册系列答案
相关题目
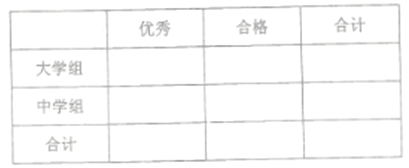
【题目】已知![]() 三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
(1)试估计![]() 班学生人数;
班学生人数;
(2)从![]() 班和
班和![]() 班抽出来的学生中各选一名,记
班抽出来的学生中各选一名,记![]() 班选出的学生为甲,
班选出的学生为甲,![]() 班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.