题目内容
数列{an}满足a1=1,a2=2,且
(1)求{an}的通项公式;
(2)数列{bn}满足 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
解:(1)∵
∴数列{an}是等差数列,
∵a1=1,a2=2,
∴公差d=1,首项a1=1,
∴an=n.
(2)∵ ,
,
=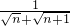
= .
.
∴
=
=
= .
.
分析:(1)由 ,知数列{an}是等差数列,由a1=1,a2=2,知公差d=1,首项a1=1,由此能求出an.
,知数列{an}是等差数列,由a1=1,a2=2,知公差d=1,首项a1=1,由此能求出an.
(2)由 ,=
,=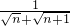 =
= .知
.知 =
= ,由此能求出
,由此能求出
数列{bn}的前n项和Sn.
点评:本题考查数列的递推公式,综合性强,难度大,容易出错.解题时要认真审题,注意合理地进行等价转化.

∴数列{an}是等差数列,
∵a1=1,a2=2,
∴公差d=1,首项a1=1,
∴an=n.
(2)∵
 ,
,=
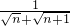
=
 .
.∴

=

=

=
 .
.分析:(1)由
 ,知数列{an}是等差数列,由a1=1,a2=2,知公差d=1,首项a1=1,由此能求出an.
,知数列{an}是等差数列,由a1=1,a2=2,知公差d=1,首项a1=1,由此能求出an.(2)由
 ,=
,=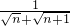 =
= .知
.知 =
= ,由此能求出
,由此能求出数列{bn}的前n项和Sn.
点评:本题考查数列的递推公式,综合性强,难度大,容易出错.解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目