题目内容
若向量 =(
=( ,1),
,1), =(0,-2),则与
=(0,-2),则与 +2
+2 共线的向量可以是
共线的向量可以是
- A.(
 ,-1)
,-1) - B.(-1,-
 )
) - C.(-
 ,-1)
,-1) - D.(-1,
 )
)
D
分析:求出2 的坐标表示,然后求解
的坐标表示,然后求解 +2
+2 ,然后判断与之共线的向量即可.
,然后判断与之共线的向量即可.
解答:向量 =(
=( ,1),
,1), =(0,-2),则2
=(0,-2),则2 =(0,-4)
=(0,-4)
所以 +2
+2 =(
=( ,-3).
,-3).
因为 (-1,
(-1, )=(
)=(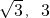 ).
).
故选D.
点评:本题考查向量的坐标运算,向量平行的判断,考查计算能力.
分析:求出2
 的坐标表示,然后求解
的坐标表示,然后求解 +2
+2 ,然后判断与之共线的向量即可.
,然后判断与之共线的向量即可.解答:向量
 =(
=( ,1),
,1), =(0,-2),则2
=(0,-2),则2 =(0,-4)
=(0,-4)所以
 +2
+2 =(
=( ,-3).
,-3).因为
 (-1,
(-1, )=(
)=(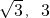 ).
).故选D.
点评:本题考查向量的坐标运算,向量平行的判断,考查计算能力.

练习册系列答案
相关题目
设向量i、j为直角坐标系的x轴、y轴正方向上的单位向量,若向量
=(x+1)i+yj,
=(x-1)i+yj,且|
|-|
|=1,则满足上述条件的点P(x,y)的轨迹方程是( )
| a |
| b |
| a |
| b |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
若向量
=(3,-1),
=(2,1),且
•
=7,那么
•
的值为( )
| AB |
| n |
| n |
| AC |
| n |
| BC |
| A、0 | B、2 | C、-2 | D、-2或2 |