题目内容
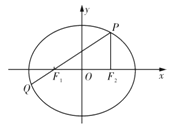
【题目】如图,在平面直角坐标系![]() 中,椭圆C:
中,椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,P为椭圆C上一点,且
,P为椭圆C上一点,且![]() 垂直于
垂直于![]() 轴,连结
轴,连结![]() 并延长交椭圆于另一点
并延长交椭圆于另一点![]() ,设
,设![]()
(1)若点![]() 的坐标为
的坐标为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)若![]() ,求椭圆
,求椭圆![]() 的离心率的取值范围
的离心率的取值范围
【答案】(1) ![]() ;(2)
;(2) ![]()
【解析】
(1)由已知可得![]() ,将点
,将点![]() 代入椭圆方程,联立求得
代入椭圆方程,联立求得![]() ,
,![]() ,则椭圆方程可求;(2)由
,则椭圆方程可求;(2)由![]() 轴,不妨设
轴,不妨设![]() ,
,![]() ,设
,设![]() ,由P在椭圆上,求得
,由P在椭圆上,求得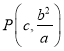 ,结合
,结合![]() ,利用向量等式求得Q坐标,结合点Q在椭圆上,列式可得
,利用向量等式求得Q坐标,结合点Q在椭圆上,列式可得![]() ,结合
,结合![]() 的范围求椭圆C的离心率的取值范围.
的范围求椭圆C的离心率的取值范围.
(1)∵![]() 垂直于
垂直于![]() 轴,且点
轴,且点![]() 的坐标为
的坐标为![]()
∴![]() ,
,![]() ,解得
,解得![]() ,
,![]()
∴椭圆C的方程为![]() .
.
(2)∵![]() 轴,不妨设
轴,不妨设![]() 在
在![]() 轴上方,
轴上方,![]() ,
,![]() ,设
,设![]()
∵P在椭圆上,∴![]() .解得
.解得![]() ,即
,即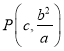
∵![]() ,由
,由![]() 得
得![]() ,
,
解得![]() ,∴
,∴![]()
∵点![]() 在椭圆上
在椭圆上
∴![]() ,即
,即![]()
∴![]() ,从而
,从而![]()
∵![]() ,∴
,∴![]()
解得![]()
∴椭圆C的离心率的取值范围是![]() .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目