题目内容
直角坐标系 和极坐标系
和极坐标系 的原点与极点重合,
的原点与极点重合, 轴正半轴与极轴重合,单位长度相同,在直角坐标系下,曲线C的参数方程为
轴正半轴与极轴重合,单位长度相同,在直角坐标系下,曲线C的参数方程为 为参数)。
为参数)。
(1)在极坐标系下,曲线C与射线 和射线
和射线 分别交于A,B两点,求
分别交于A,B两点,求 的面积;
的面积;
(2)在直角坐标系下,直线 的参数方程为
的参数方程为 (
( 为参数),求曲线C与直线
为参数),求曲线C与直线 的交点坐标。
的交点坐标。
【答案】
(1) (2)(2
(2)(2 ,
, )
)
【解析】
试题分析:(Ⅰ)曲线C在直角坐标系下的普通方程为 +
+ =1,将其化为极坐标方程为
=1,将其化为极坐标方程为
分别代入θ= 和θ=-
和θ=- ,得|OA|2=|OB|2=
,得|OA|2=|OB|2= ,
,
因∠AOB= ,故△AOB的面积S=
,故△AOB的面积S= |OA||OB|=
|OA||OB|= .
5分
.
5分
(Ⅱ)将l的参数方程代入曲线C的普通方程,得(t-2 )2=0,
)2=0,
∴t=2 ,代入l的参数方程,得x=2
,代入l的参数方程,得x=2 ,y=
,y= ,
,
所以曲线C与直线l的交点坐标为(2 ,
, ). 10分
). 10分
考点:参数方程,极坐标方程与普通方程的转化及直线与圆锥曲线的位置关系
点评:极坐标 与直角坐标的互化
与直角坐标的互化 ,极坐标方程参数方程常与圆锥曲线联系到一起考察
,极坐标方程参数方程常与圆锥曲线联系到一起考察

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
在符合互化条件的直角坐标系和极坐标系中,直线l:y+kx+2=0与曲线C:ρ=2cosθ相交,则k的取值范围是( )
A、k<-
| ||
B、k≥-
| ||
| C、k∈R | ||
| D、k∈R但k≠0 |
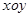 和极坐标系
和极坐标系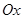 的原点与极点重合,
的原点与极点重合,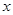 轴的正半轴与极轴重合,单位长度相同。已知曲线
轴的正半轴与极轴重合,单位长度相同。已知曲线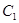 的极坐标方程为
的极坐标方程为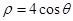 ,曲线
,曲线 的参数方程为
的参数方程为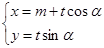
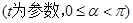 ,射线
,射线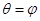 ,
,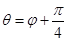 ,
,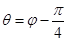 与曲线
与曲线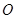 以外的三点A,B,C.
以外的三点A,B,C.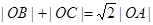 ;
;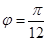 时,B,C两点在曲线
时,B,C两点在曲线 与
与 的值。
的值。 与曲线C:
与曲线C: 相交,则k的取值范围是( ).
相交,则k的取值范围是( ). B.
B.
 C.
C.
 D.
D.

 和极坐标系
和极坐标系 的原点与极点重合,
的原点与极点重合, 轴正半轴与极轴重合,单位长度相同,在直角坐标系下,曲线C的参数方程为
轴正半轴与极轴重合,单位长度相同,在直角坐标系下,曲线C的参数方程为 为参数)。
为参数)。 和射线
和射线 分别交于A,B两点,求
分别交于A,B两点,求 的面积;
的面积; 的参数方程为
的参数方程为 (
( 为参数),求曲线C与直线
为参数),求曲线C与直线