题目内容
已知|
|=|
|=1，
•
=0，点C满足
=λ
+μ
（λ，μ∈R+），且∠AOC=30°，则
等于（ ）
| OA |
| OB |
| OA |
| OB |
| OC |
| OA |
| OB |
| λ |
| μ |
分析：由题意，以OA、OB分别为x轴和y轴，建立如图所求直角坐标系．由∠AOC=30°，可设C（
a，a），根据点C满足
=λ
+μ
建立关于λ、μ的方程组，解之即可得到
的值．
| 3 |
| OC |
| OA |
| OB |
| λ |
| μ |
解答：解：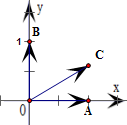
∵
•
=0，∴
⊥
，
因此以O为原点，OA、OB分别为x轴和y轴，建立如图所求直角坐标系．
∵∠AOC=30°，
∴可得tan∠AOC=
，
∵点C在直线y=
x上，
∴可设C（
a，a），
∵|
|=|
|=1，
∴
=（1，0），
=（0，1），
∵点C满足
=λ
+μ
（λ，μ∈R+），
∴由平面向量基本定理，
得
，可得
=
．
故选：D
∵| OA |
| OB |
| OA |
| OB |
因此以O为原点，OA、OB分别为x轴和y轴，建立如图所求直角坐标系．
∵∠AOC=30°，
∴可得tan∠AOC=
| ||
| 3 |
∵点C在直线y=
| ||
| 3 |
∴可设C（
| 3 |
∵|
| OA |
| OB |
∴
| OA |
| OB |
∵点C满足
| OC |
| OA |
| OB |
∴由平面向量基本定理，
得
|
| λ |
| μ |
| 3 |
故选：D
点评：本题给出互相垂直的单位向量
、
，在点C满足∠AOC=30°的情况下，求参数
的值．着重考查了向量的坐标运算与平面向量基本定理等知识，属于中档题．
| OA |
| OB |
| λ |
| μ |
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
如图，设点A和B为抛物线y2=4px（p＞0）上原点以外的两个动点，已知OA⊥OB，OM⊥AB．求点M的轨迹方程，并说明它表示什么曲线．
（2013•潮州二模）如图，已知OA=OB=OC，∠ACB=45°，则∠OBA的大小为