题目内容
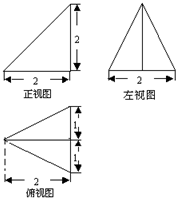
已知某个几何体的三视图如图：则这个几何体的侧面中，等腰三角形的个数是（ ）分析：由俯视图看出，原几何体的底面是等腰三角形，俯视图内部的实线应该是原几何体的一条侧棱在底面上的射影，且原几何体的顶点在底面的射影是底面等腰三角形的底边中点，然后结合正视图和侧视图可得原实物图，最后根据三视图中的数据可求得原几何体的侧棱长和底面边长，从而判断出各侧面的形状．
解答：解：由三视图还原实物图如图，
再由三视图中的数据可知，
AD⊥BC，PD⊥BC，BD=DC=1，AD=PD=2，
所以，在直角三角形ADB中，AB=
=
=
，
在直角三角形PDB中，PB=
=
=
，
在直角三角形ADC中，AC=
=
=
，
在直角三角形PDC中，PC=
=
=
．
所以，这个几何体的侧面中，等腰三角形分别是△PBC、△BPA、△CPA共三个．
故选C．
再由三视图中的数据可知，
AD⊥BC，PD⊥BC，BD=DC=1，AD=PD=2，
所以，在直角三角形ADB中，AB=
| AD2+DB2 |
| 12+22 |
| 5 |
在直角三角形PDB中，PB=
| PD2+DB2 |
| 12+22 |
| 5 |
在直角三角形ADC中，AC=
| AD2+DC2 |
| 12+22 |
| 5 |
在直角三角形PDC中，PC=
| PD2+DC2 |
| 12+22 |
| 5 |
所以，这个几何体的侧面中，等腰三角形分别是△PBC、△BPA、△CPA共三个．
故选C．
点评：本题考查了由三视图还原实物图，还原实物图的方法是：首先看俯视图，然后结合正视图和侧视图得原图形，本题考查了学生的空间想象和思维能力，此题属中档题．
练习册系列答案
相关题目
已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是
已知某个几何体的三视图如图，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（ ）
（1）已知某个几何体的三视图如图（主视图的弧线是半圆），根据图中的数据，求这个组合体的体积；
已知某个几何体的三视图如图，根据图中标出的尺寸（单位：cm），可得这个几何体的表面积是（ ）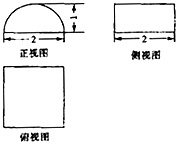
已知某个几何体的三视图如图（正视图中的弧线是半圆），图中标出的尺（单位：cm），可得这个几何体表面是