题目内容
已知f(x)=|x+1|+|x-1|,不等式f(x)的解集为M.
(1)求M;
(2)当a,b M时,证明:2|a+b|<|4+ab|.
M时,证明:2|a+b|<|4+ab|.
(1) ;(2)证明过程详见解析.
;(2)证明过程详见解析.
解析试题分析:本题主要考查绝对值不等式、不等式的证明等基础知识,意在考查考生的运算求解能力、利用综合法、分类讨论思想的解题能力.第一问,利用零点分段法分别去掉绝对值,解不等式;第二问,可先用分析法由所求证的结论入手,分析需要证明什么,再用综合法证明,要证2|a+b|<|4+ab|,需证明 ,展开,需证明
,展开,需证明 ,由已知入手,找到
,由已知入手,找到 ,
, ,从而证出
,从而证出 .
.
试题解析:(1)由 ,即
,即 ,
,
当 时,则
时,则 ,得
,得 ,∴
,∴ ;
;
当 时,则
时,则 ,得
,得 ,恒成立,∴
,恒成立,∴ ;
;
当 时,则
时,则 ,得
,得 ,∴
,∴ ;
;
综上, . 5分
. 5分
(2)当 时,则
时,则 ,
, .
.
即: ,
, ,∴
,∴ ,
,
∴ ,即
,即 ,
,
也就是 ,
,
∴ ,
,
即: ,
,
即 . 10分
. 10分
考点:绝对值不等式、不等式的证明.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 ,(1)当a=2时,求关于x的不等式
,(1)当a=2时,求关于x的不等式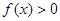 的解集;(2)当a>0时,求关于x的不等式
的解集;(2)当a>0时,求关于x的不等式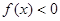 的解集.
的解集. ,求函数y=4x-2+
,求函数y=4x-2+ 的最大值;
的最大值; =1,求x+y的最小值.
=1,求x+y的最小值. 的不等式
的不等式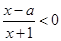 的解集为
的解集为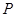 ,不等式
,不等式 的解集为
的解集为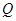 .
.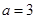 ,求
,求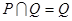 ,求正数
,求正数 的取值.
的取值. 使不等式
使不等式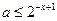 在
在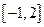 成立,则
成立,则