题目内容
设函数 .
.
(1)求函数f(x)的最小正周期T,并求出函数f(x)的单调递增区间;
(2)求在[0,3π)内使f(x)取到最大值的所有x的和.
解:(1)∵f(x)= cos2x+sinxcosx-
cos2x+sinxcosx-
= +
+ sin2x-
sin2x-
= cos2x+
cos2x+ sin2x
sin2x
=sin(2x+ ),…(2分)
),…(2分)
故T=π,…(4分)
∵2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,
∴kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,
∴f(x)的单调递增区间为:[kπ- ,kπ+
,kπ+ ](k∈Z)…(6分)
](k∈Z)…(6分)
(2)∵f(x)=1即sin(2x+ )=1,则2x+
)=1,则2x+ =2kπ+
=2kπ+ ,
,
∴x=kπ+ (k∈Z)…(8分)
(k∈Z)…(8分)
∵0≤x<3π,
∴k=0,1,2…(10分)
∴在[0,3π)内使f(x)取到最大值的所有x的和为 …(12分)
…(12分)
分析:(1)利用两角和与差的三角函数将f(x)= cos2x+sinxcosx-
cos2x+sinxcosx- 化为f(x)=sin(2x+
化为f(x)=sin(2x+ ),即可求得函数f(x)的最小正周期T及函数f(x)的单调递增区间;
),即可求得函数f(x)的最小正周期T及函数f(x)的单调递增区间;
(2)由f(x)=sin(2x+ )=1可求得x,由x∈[0,3π)即可求得f(x)取到最大值的所有x的和.
)=1可求得x,由x∈[0,3π)即可求得f(x)取到最大值的所有x的和.
点评:本题考查两角和与差的三角函数,考查正弦函数的单调性与最值,考查规范答题与运算能力,属于中档题.
 cos2x+sinxcosx-
cos2x+sinxcosx-
=
 +
+ sin2x-
sin2x-
=
 cos2x+
cos2x+ sin2x
sin2x=sin(2x+
 ),…(2分)
),…(2分)故T=π,…(4分)
∵2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,∴kπ-
 ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,∴f(x)的单调递增区间为:[kπ-
 ,kπ+
,kπ+ ](k∈Z)…(6分)
](k∈Z)…(6分)(2)∵f(x)=1即sin(2x+
 )=1,则2x+
)=1,则2x+ =2kπ+
=2kπ+ ,
,∴x=kπ+
 (k∈Z)…(8分)
(k∈Z)…(8分)∵0≤x<3π,
∴k=0,1,2…(10分)
∴在[0,3π)内使f(x)取到最大值的所有x的和为
 …(12分)
…(12分)分析:(1)利用两角和与差的三角函数将f(x)=
 cos2x+sinxcosx-
cos2x+sinxcosx- 化为f(x)=sin(2x+
化为f(x)=sin(2x+ ),即可求得函数f(x)的最小正周期T及函数f(x)的单调递增区间;
),即可求得函数f(x)的最小正周期T及函数f(x)的单调递增区间;(2)由f(x)=sin(2x+
 )=1可求得x,由x∈[0,3π)即可求得f(x)取到最大值的所有x的和.
)=1可求得x,由x∈[0,3π)即可求得f(x)取到最大值的所有x的和.点评:本题考查两角和与差的三角函数,考查正弦函数的单调性与最值,考查规范答题与运算能力,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 设函数
设函数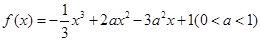 ,
,
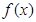 的极大值;
的极大值; ,若
,若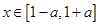 时,恒有
时,恒有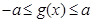 成立,试确定实数
成立,试确定实数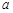 的取值范围.
的取值范围.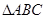 中,角
中,角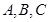 的对边分别为
的对边分别为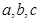 ,且
,且
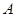 ;
;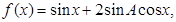 将函数
将函数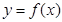 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的 ,把所得图象向右平移
,把所得图象向右平移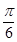 个单位,得到函数
个单位,得到函数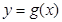 的图象,求函数
的图象,求函数