题目内容
在区间D上,如果函数f(x)为增函数,而函数 为减函数,则称函数f(x)为“弱增函数”.已知函数f(x)=1-
为减函数,则称函数f(x)为“弱增函数”.已知函数f(x)=1- .
.
(1)判断函数f(x)在区间(0,1]上是否为“弱增函数”;
(2)设x1,x2∈[0,+∞),且x1≠x2,证明:|f(x2)-f(x1)|<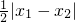 ;
;
(3)当x∈[0,1]时,不等式1-ax≤ ≤1-bx恒成立,求实数a,b的取值范围.
≤1-bx恒成立,求实数a,b的取值范围.
解:(1)显然f(x)在区间上为增函数(0,1],
因为 =
=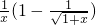 =
=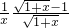 =
=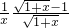 =
=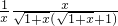 =
=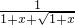 ,
,
所以 在区间(0,1]上为减函数.
在区间(0,1]上为减函数.
所以f(x)在区间(0,1]上为“弱减函数”.
(2)证法1:要证|f(x2)-f(x1)|<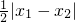 ,不妨设0≤x1<x2,
,不妨设0≤x1<x2,
由f(x)=1- 在[0,+∞)单调递增,
在[0,+∞)单调递增,
得f(x2)>f(x1),
那么只要证f(x2)-f(x1)<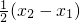 ,
,
即证f(x2)-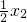 <f(x1)-
<f(x1)- .
.
令g(x)=f(x)- ,则问题转化为只要证明g(x)=f(x)-
,则问题转化为只要证明g(x)=f(x)- 在[0,+∞)单调递减即可.
在[0,+∞)单调递减即可.
事实上,g(x)=f(x)- =1-
=1- -
- ,
,
当x∈[0,+∞)时,g′(x)=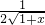 -
- ≤0,
≤0,
所以g(x)=f(x)- 在[0,+∞)单调递减,
在[0,+∞)单调递减,
故命题成立.
证法2:|f(x2)-f(x1)|= =
=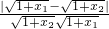
=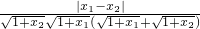 ,
,
因为x1,x2∈[0,+∞),且x1≠x2,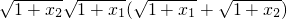 >2,
>2,
所以|f(x2)-f(x1)|<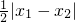 .
.
(3)当x∈[0,1]时,不等式1-ax≤ ≤1-bx恒成立.
≤1-bx恒成立.
当x=0时,不等式显然成立.
当x∈(0,1]时,等价于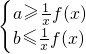 恒成立.
恒成立.
由(1)知 为减函数,1-
为减函数,1- ≤
≤ <
< ,
,
所以a≥ 且b≤1-
且b≤1- .
.
分析:(1)根据弱增函数的定义,只需证明函数f(x)在区间(0,1]上是增函数,而函数 为减函数,即可;
为减函数,即可;
(2)证法1:要证|f(x2)-f(x1)|<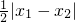 ,不妨设0≤x1<x2,构造函数g(x)=f(x)-
,不妨设0≤x1<x2,构造函数g(x)=f(x)- ,利用导数证明该函数在(0,+∞)单调递减即可证明结论;
,利用导数证明该函数在(0,+∞)单调递减即可证明结论;
证法2:把f(x)=1- 代入|f(x2)-f(x1)|,利用分母有理化,即可证明结论;
代入|f(x2)-f(x1)|,利用分母有理化,即可证明结论;
(3)要解)当x∈[0,1]时,不等式1-ax≤ ≤1-bx恒成立,利用分离参数转化为当x∈(0,1]时,等价于
≤1-bx恒成立,利用分离参数转化为当x∈(0,1]时,等价于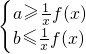 恒成立,即可求得实数a,b的取值范围.
恒成立,即可求得实数a,b的取值范围.
点评:此题是个难题.考查基本初等函数的单调性,以及构造函数证明不等式和恒成立问题,综合性强,方法灵活,很好的考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.
因为
 =
=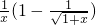 =
=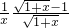 =
=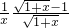 =
=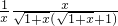 =
=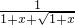 ,
,所以
 在区间(0,1]上为减函数.
在区间(0,1]上为减函数.所以f(x)在区间(0,1]上为“弱减函数”.
(2)证法1:要证|f(x2)-f(x1)|<
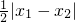 ,不妨设0≤x1<x2,
,不妨设0≤x1<x2,由f(x)=1-
 在[0,+∞)单调递增,
在[0,+∞)单调递增,得f(x2)>f(x1),
那么只要证f(x2)-f(x1)<
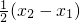 ,
,即证f(x2)-
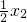 <f(x1)-
<f(x1)- .
.令g(x)=f(x)-
 ,则问题转化为只要证明g(x)=f(x)-
,则问题转化为只要证明g(x)=f(x)- 在[0,+∞)单调递减即可.
在[0,+∞)单调递减即可.事实上,g(x)=f(x)-
 =1-
=1- -
- ,
,当x∈[0,+∞)时,g′(x)=
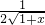 -
- ≤0,
≤0,所以g(x)=f(x)-
 在[0,+∞)单调递减,
在[0,+∞)单调递减,故命题成立.
证法2:|f(x2)-f(x1)|=
 =
=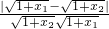
=
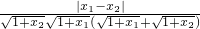 ,
,因为x1,x2∈[0,+∞),且x1≠x2,
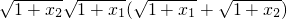 >2,
>2,所以|f(x2)-f(x1)|<
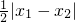 .
.(3)当x∈[0,1]时,不等式1-ax≤
 ≤1-bx恒成立.
≤1-bx恒成立.当x=0时,不等式显然成立.
当x∈(0,1]时,等价于
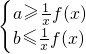 恒成立.
恒成立.由(1)知
 为减函数,1-
为减函数,1- ≤
≤ <
< ,
,所以a≥
 且b≤1-
且b≤1- .
.分析:(1)根据弱增函数的定义,只需证明函数f(x)在区间(0,1]上是增函数,而函数
 为减函数,即可;
为减函数,即可;(2)证法1:要证|f(x2)-f(x1)|<
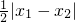 ,不妨设0≤x1<x2,构造函数g(x)=f(x)-
,不妨设0≤x1<x2,构造函数g(x)=f(x)- ,利用导数证明该函数在(0,+∞)单调递减即可证明结论;
,利用导数证明该函数在(0,+∞)单调递减即可证明结论;证法2:把f(x)=1-
 代入|f(x2)-f(x1)|,利用分母有理化,即可证明结论;
代入|f(x2)-f(x1)|,利用分母有理化,即可证明结论;(3)要解)当x∈[0,1]时,不等式1-ax≤
 ≤1-bx恒成立,利用分离参数转化为当x∈(0,1]时,等价于
≤1-bx恒成立,利用分离参数转化为当x∈(0,1]时,等价于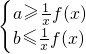 恒成立,即可求得实数a,b的取值范围.
恒成立,即可求得实数a,b的取值范围.点评:此题是个难题.考查基本初等函数的单调性,以及构造函数证明不等式和恒成立问题,综合性强,方法灵活,很好的考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

练习册系列答案
相关题目
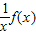 为减函数,则称函数f(x)为“弱增”函数.已知函数
为减函数,则称函数f(x)为“弱增”函数.已知函数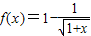 .
.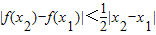 ;
;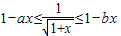 恒成立,求实数a,b的取值范围.
恒成立,求实数a,b的取值范围. 为减函数,则称函数f(x)为“弱增函数”.已知函数f(x)=1-
为减函数,则称函数f(x)为“弱增函数”.已知函数f(x)=1-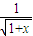 .
. ;
; ≤1-bx恒成立,求实数a,b的取值范围.
≤1-bx恒成立,求实数a,b的取值范围.