题目内容
在区间D上,如果函数f(x)为增函数,而函数| 1 |
| x |
| 1 | ||
|
(1)判断函数f(x)在区间(0,1]上是否为“弱增”函数;
(2)设x1,x2∈[0,+∞),x1≠x2,证明|f(x2)-f(x1)|<
| 1 |
| 2 |
(3)当x∈[0,1]时,不等式1-ax≤
| 1 | ||
|
分析:(1)显然f(x)在区间(0,1]为增函数,化简
f(x)的解析式为
,显然是减函数,可得f(x)在区间(0,1]为“弱增”函数.
(2)化简|f(x2)-f(x1)|的解析式为
,由,即可证得命题成立.
(3)当x∈(0,1]时,不等式等价于:
,由
f(x)为减函数,可得1-
≤
f(x)<
,从而求得实数a,b的取值范围.
| 1 |
| x |
| 1 | ||
1+x+
|
(2)化简|f(x2)-f(x1)|的解析式为
| |x2-x1| | ||||||||
|
(3)当x∈(0,1]时,不等式等价于:
|
| 1 |
| x |
| ||
| 2 |
| 1 |
| x |
| 1 |
| 2 |
解答:解:(1)显然f(x)在区间(0,1]为增函数,
∵
f(x)=
(1-
)=
=
=
,
∴
f(x)为减函数.∴f(x)在区间(0,1]为“弱增”函数.
(2)|f(x2)-f(x1)|=|
-
|=
=
,
∵x1,x2∈[0,+∞),x1≠x2,
(
+
)>2,
∴|f(x2)-f(x1)|<
|x2-x1|.
(3)∵当x∈[0,1]时,不等式1-ax≤
≤1-bx恒成立. 当x=0时,不等式显然成立.
当x∈(0,1]时.等价于:
,
由(1)
f(x)为减函数,1-
≤
f(x)<
,∴a≥
,b≤1-
.
∵
| 1 |
| x |
| 1 |
| x |
| 1 | ||
|
| 1 |
| x |
| ||
|
| 1 |
| x |
| x | ||||
|
| 1 | ||
1+x+
|
∴
| 1 |
| x |
(2)|f(x2)-f(x1)|=|
| 1 | ||
|
| 1 | ||
|
|
| ||||
|
| |x2-x1| | ||||||||
|
∵x1,x2∈[0,+∞),x1≠x2,
| 1+x2 |
| 1+x1 |
| 1+x2 |
| 1+x1 |
∴|f(x2)-f(x1)|<
| 1 |
| 2 |
(3)∵当x∈[0,1]时,不等式1-ax≤
| 1 | ||
|
当x∈(0,1]时.等价于:
|
由(1)
| 1 |
| x |
| ||
| 2 |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查函数的单调性的判断和证明,不等式的证明,体现了分类讨论的数学思想,得到当x∈(0,1]时.等价于:
,是解题的难点.
|

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
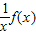 为减函数,则称函数f(x)为“弱增”函数.已知函数
为减函数,则称函数f(x)为“弱增”函数.已知函数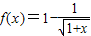 .
.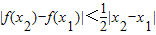 ;
;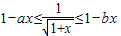 恒成立,求实数a,b的取值范围.
恒成立,求实数a,b的取值范围. 为减函数,则称函数f(x)为“弱增函数”.已知函数f(x)=1-
为减函数,则称函数f(x)为“弱增函数”.已知函数f(x)=1-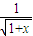 .
. ;
; ≤1-bx恒成立,求实数a,b的取值范围.
≤1-bx恒成立,求实数a,b的取值范围.