题目内容
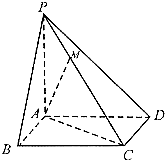（2011•武昌区模拟）如图，四棱锥P-ABCD的底面的正方形，侧棱PA⊥底面ABCD，PA=| 2 |
（Ⅰ）求直线AM与平面ABCD所成角的正切值；
（Ⅱ）求二面角A-PC-D的余弦值．
分析：（Ⅰ）过M作MN⊥AC于N，则MN∥PA，根据侧棱PA⊥底面ABCD，可得MN⊥底面ABCD，从而∠MAN为直线AM与平面ABCD所成的角，在Rt△AMN中，可求直线AM与平面ABCD所成的角正切值；
（Ⅱ）过A作AE⊥PD于E，过A作AF⊥PC于F，连接EF，则∠AFE为二面角A-PC-D的平面角，在Rt△AEF中，可求二面角的余弦值．
（Ⅱ）过A作AE⊥PD于E，过A作AF⊥PC于F，连接EF，则∠AFE为二面角A-PC-D的平面角，在Rt△AEF中，可求二面角的余弦值．
解答：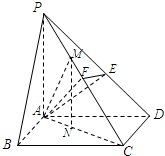
解：设PA=
AB=
．
（Ⅰ）过M作MN⊥AC于N，则MN∥PA．
∵侧棱PA⊥底面ABCD
∴MN⊥底面ABCD．
则∠MAN为直线AM与平面ABCD所成的角．…（2分）
∵CM=2MP，CN=2NA．
∴AC=
∴AN=
．
又
=
，
∴MN=
．
在Rt△AMN中，得tan∠MAN=
=2．
所以，直线AM与平面ABCD所成的角正切值为2．…（6分）
（Ⅱ）过A作AE⊥PD于E．
∵侧棱PA⊥底面ABCD，CD?底面ABCD
∴PA⊥CD．
∵CD⊥AD，PA∩AD=A
∴CD⊥面PAD．
∵AE?面PAD
∴CD⊥AE
∵PD∩CD=D
∴AE⊥面PCD．
过A作AF⊥PC于F，连接EF．
则∠AFE为二面角A-PC-D的平面角．…（8分）
∵AE=
，AF=1．
∴在Rt△AEF中，得sin∠AFE=
=
．
∴cos∠AFE=
所以，所求二面角的余弦值为
．…（12分）
解：设PA=| 2 |
| 2 |
（Ⅰ）过M作MN⊥AC于N，则MN∥PA．
∵侧棱PA⊥底面ABCD
∴MN⊥底面ABCD．
则∠MAN为直线AM与平面ABCD所成的角．…（2分）
∵CM=2MP，CN=2NA．
∴AC=
| 2 |
∴AN=
| ||
| 3 |
又
| MN |
| PA |
| 2 |
| 3 |
∴MN=
2
| ||
| 3 |
在Rt△AMN中，得tan∠MAN=
| MN |
| AN |
所以，直线AM与平面ABCD所成的角正切值为2．…（6分）
（Ⅱ）过A作AE⊥PD于E．
∵侧棱PA⊥底面ABCD，CD?底面ABCD
∴PA⊥CD．
∵CD⊥AD，PA∩AD=A
∴CD⊥面PAD．
∵AE?面PAD
∴CD⊥AE
∵PD∩CD=D
∴AE⊥面PCD．
过A作AF⊥PC于F，连接EF．
则∠AFE为二面角A-PC-D的平面角．…（8分）
∵AE=
| ||
|
∴在Rt△AEF中，得sin∠AFE=
| AE |
| AF |
| ||
| 3 |
∴cos∠AFE=
| ||
| 3 |
所以，所求二面角的余弦值为
| ||
| 3 |
点评：本题以四棱锥为载体，考查线面角，面面角，解题的关键是正确作出线面角，面面角，构建三角形进行求解．
练习册系列答案
相关题目