题目内容
已知函数 .
.
(1)求函数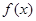 的定义域
的定义域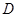 ,并判断
,并判断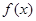 的奇偶性;
的奇偶性;
(2)用定义证明函数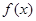 在
在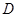 上是增函数;
上是增函数;
(3)如果当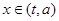 时,函数
时,函数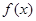 的值域是
的值域是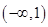 ,求
,求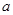 与
与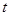 的值.
的值.
【答案】
.解:(1)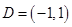 ,函数
,函数 是奇函数.
是奇函数.
(2)设、算、证、结
(3)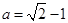 ,
,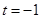
【解析】
试题分析:
思路分析:(1)由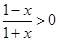 ,求得
,求得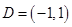
计算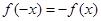 知函数
知函数 是奇函数.
是奇函数.
另证:对任意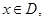
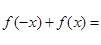 0,
0,
(2)利用“定义”“设、算、证、结”。
(3)根据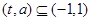 且
且 在
在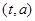 的值域是
的值域是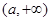 ,
,
得到a的方程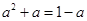 解得
解得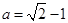 (
( 舍去)
舍去)
得到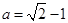 ,
,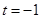 。
。
解:(1)令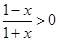 ,解得
,解得 ,
,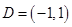
对任意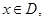
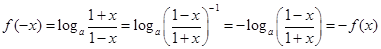
所以函数 是奇函数.
是奇函数.
另证:对任意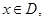
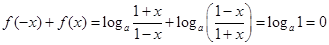 ,
,
所以函数 是奇函数.
是奇函数.
(2)设 ,
,
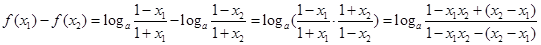
∴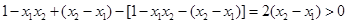
∴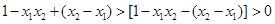
∴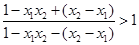 ∵
∵ ∴
∴
∴ ,∴
,∴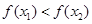
所以函数 在
在 上是增函数.
上是增函数.
(3)由(2)知,函数 在
在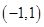 上是增函数,
上是增函数,
又因为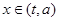 时,
时, 的值域是
的值域是 ,
,
所以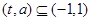 且
且 在
在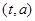 的值域是
的值域是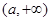 ,
,
故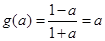 且
且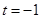 (结合
(结合 图像易得
图像易得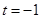 )
)
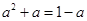 解得
解得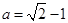 (
( 舍去)
舍去)
所以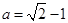 ,
,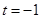
考点:对数函数的性质,函数的奇偶性、单调性。
点评:中档题,本题主要考查对数函数的性质,利用函数的奇偶性、单调性定义,判断函数的奇偶性,证明函数的单调性,属于基础题目。

练习册系列答案
相关题目
 .
. 的定义域
;
的定义域
; ,求实数
,求实数 的值.
的值. .
. 在(0,+∞)上是减函数.
在(0,+∞)上是减函数.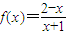 ;
; 成立,若存在求出x;若不存在,请说明理由.
成立,若存在求出x;若不存在,请说明理由. 令
令
 的定义域;
的定义域; 的奇偶性,并予以证明;
的奇偶性,并予以证明; ,猜想
,猜想 之间的关系并证明.
之间的关系并证明. ,
, 的定义域;(2)证明:
的定义域;(2)证明: ,求
,求 的取值范围。
的取值范围。