题目内容
12．函数f（x）=tan（$\frac{1}{3}x$+$\frac{π}{6}$）的最小正周期为（ ）| A． | 3π | B． | 6π | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |
分析 利用三角函数的周期性及其求法即可得解．
解答 解：最小正周期T=$\frac{π}{\frac{1}{3}}=3π$．
故选：A．
点评 本题主要考查了三角函数的周期性及其求法，考查周期公式的应用，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
2．若q＜19，则将（x-q）（x-q-1）（x-q-2）•…•（x-19）写成A${\;}_{n}^{m}$的形式是（ ）
| A． | A${\;}_{x-q}^{x-19}$ | B． | A${\;}_{x-q}^{x-20}$ | C． | A${\;}_{x-q}^{19-q}$ | D． | A${\;}_{x-q}^{20-q}$ |
3．复数z=$\frac{5i}{1-2i}$（i为虚数单位）的共轭复数$\overline{z}$等于（ ）
| A． | -1-2i | B． | 1+2i | C． | 2-i | D． | -2-i |
20．已知扇形的圆心角为$\frac{3}{4}π$，半径为4，则扇形的面积S为（ ）
| A． | 3π | B． | 4π | C． | 6π | D． | 2π |
7．
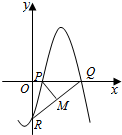如图，函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|≤$\frac{π}{2}$）与坐标轴的三个交点P、Q、R满足P（1，0），M（2，-2）为线段QR的中点，则A=（ ）
如图，函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|≤$\frac{π}{2}$）与坐标轴的三个交点P、Q、R满足P（1，0），M（2，-2）为线段QR的中点，则A=（ ）| A． | 2$\sqrt{3}$ | B． | $\frac{7\sqrt{3}}{3}$ | C． | $\frac{8\sqrt{3}}{3}$ | D． | 4$\sqrt{3}$ |
17．从1，2，3，4，5这5个数中取出2个数，使得剩下的3个数的平均数与原来5个数的平均数不变，则不同的取法共有（ ）
| A． | 1种 | B． | 2种 | C． | 3种 | D． | 4种 |