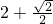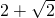题目内容
设直线x+y=2a-1与圆x2+y2=a2+2a-3的交点为(x,y),当x+y取得最小值时,实数a的值为( )A.
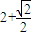
B.
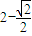
C.
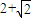
D.
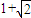
【答案】分析:由直线x+y=2a-1与圆x2+y2=a2+2a-3的交点为(x,y)表示:直线应该与圆有交点,即原点到直线的距离小于或等于圆的半径且圆的半径应该是为正数,由此求出实数a的范围,结合x+y=2a-1,进而得到答案.
解答:解:∵x2+y2=a2+2a-3表示一个圆
故a2+2a-3>0
即a<-3,或a>1…①
若直线x+y=2a-1与圆x2+y2=a2+2a-3有交点
则
即2a2-8a+7≤0
即2- ≤a≤2+
≤a≤2+ …②
…②
由①②可得2- ≤a≤2+
≤a≤2+
又∵x+y=2a-1
故当x=2- 时,x+y取得最小值
时,x+y取得最小值
故选B
点评:本题考查的知识点是直线与圆的位置关系,圆的标准方程,函数的最值及其几何意义,其中根据已知求出实数a的范围,是解答本题的关键.
解答:解:∵x2+y2=a2+2a-3表示一个圆
故a2+2a-3>0
即a<-3,或a>1…①
若直线x+y=2a-1与圆x2+y2=a2+2a-3有交点
则

即2a2-8a+7≤0
即2-
 ≤a≤2+
≤a≤2+ …②
…②由①②可得2-
 ≤a≤2+
≤a≤2+
又∵x+y=2a-1
故当x=2-
 时,x+y取得最小值
时,x+y取得最小值故选B
点评:本题考查的知识点是直线与圆的位置关系,圆的标准方程,函数的最值及其几何意义,其中根据已知求出实数a的范围,是解答本题的关键.

练习册系列答案
相关题目