题目内容
已知方程x2+y2-2(m+3)x+2(1-4m2)y+16m4+9=0表示一个圆.(1)求实数m的取值范围;
(2)求该圆半径r的取值范围;
(3)求圆心C的轨迹方程.
解:(1)∵已知方程表示圆的充要条件是
D2+E2-4F=4(m+3)2+4(1-4m2)2-4(16m4+9)＞0.
解得-
＜m＜1.
(2)∵圆半径r=
≤
,∴0＜r≤
为所求.
(3)设圆心为C(x,y),则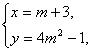
消去m得y=4(x-3)2-1.
又∵-
＜m＜1,
∴
＜x＜4.
故所求圆心C的轨迹为y=4(x-3)2-1且
＜x＜4.
练习册系列答案
名校课堂系列答案
相关题目