题目内容
在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.求证:PA∥平面EDB.
证明：建立如图所示的空间直角坐标系,
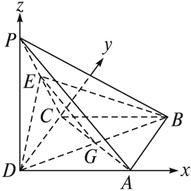
连结AC交BD于G,连结EG.
设DC=a,依题意得A(a,0,0),
P(0,0,a),E(0,
).
∵底面ABCD是正方形,
∴G是此正方形的中心,故点G的坐标为(
,0).
∴
=(a,0,-a),
=(
).
PA=2EG,这表明PA∥EG.
而EG
平面EDB且PA
平面EDB.
∴PA∥平面EDB.
练习册系列答案
名校课堂系列答案
相关题目
如图，在四棱锥P-ABCD中，底面为直角梯形，AD∥BC，∠BAD=90，PA⊥底面ABCD，且PA=AD=AB=2BC=2，M，N分别为PC、PB的中点．
如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4．AB=2，AN⊥PC于点N，M是PD中点．
如图，在四棱锥P-ABCD中，底面ABCD是矩形，O为底面中心，PA⊥平面ABCD，PA=AD=2AB．M是PD的中点
如图，在四棱锥P-ABCD中，底面ABCD是矩形，已知AB=3，AD=2，PA=2，PD=2
（2009•成都模拟）如图，在四棱锥P-ABCD中，底面ABCD为正方形，且PD⊥平面ABCD，PD=AB=1，EF分别是PB、AD的中点，