题目内容
【题目】
已知函数![]() ,其中
,其中![]() ,记函数
,记函数![]() 的定义域为
的定义域为![]() .
.
(1)求函数![]() 的定义域
的定义域![]() ;
;
(2)若函数![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值;
的值;
(3)若对于![]() 内的任意实数
内的任意实数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() .
.
(2) ![]() .
.
(3) ![]() .
.
【解析】分析:(1)根据使函数的解析式有意义的原则,构造关于自变量![]() 的不等式组,即可求解函数的定义域;
的不等式组,即可求解函数的定义域;
(2)利用对数函数的运算性质,化简函数的解析式,并根据二次函数的图象与性质,可分析出函数的最小值为![]() 时,即可求解实数
时,即可求解实数![]() 的值.
的值.
(3)若不等式![]() 恒成立,即
恒成立,即![]() 在
在![]() 上恒成立,设出新函数
上恒成立,设出新函数![]() ,利用基本不等式求解最大值,即可求解实数
,利用基本不等式求解最大值,即可求解实数![]() 的取值范围.
的取值范围.
详解:(1)要使函数有意义:则有![]() ,解得-2<x<1
,解得-2<x<1
∴ 函数的定义域![]() 为
为![]()
(2)![]()
因为 ![]()
所以 ![]()
因为![]() ,所以
,所以![]() ,
,
即![]() ,
,
由![]() ,得
,得![]() ,
,
(3)由![]() 在
在![]() 恒成立,
恒成立,
得 ![]()
因为![]() ,所以
,所以![]()
所以![]() 在
在![]() 恒成立
恒成立
设![]() ,令
,令![]()
则![]()
即![]() ,因为
,因为![]() ,
,
所以![]() (当且仅当
(当且仅当![]() 时,取等号
时,取等号
所以![]()
所以![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为原点,
为原点,![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线的
,求直线的![]() 斜率的取值范围.
斜率的取值范围.
【题目】某水仙花经营部每天的房租、水电、人工等固定成本为1000元,每盆水仙花的进价是10元,销售单价![]() (元) (
(元) (![]() )与日均销售量
)与日均销售量![]() (盆)的关系如下表,并保证经营部每天盈利.
(盆)的关系如下表,并保证经营部每天盈利.
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
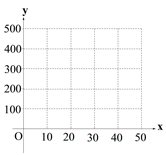
(Ⅰ) 在所给的坐标图纸中,根据表中提供的数据,描出实数对![]() 的对应点,并确定
的对应点,并确定![]() 与
与![]() 的函数关系式;
的函数关系式;
(Ⅱ)求出![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(Ⅲ)请写出该经营部的日销售利润![]() 的表达式,并回答该经营部怎样定价才能获最大日销售利润?
的表达式,并回答该经营部怎样定价才能获最大日销售利润?