题目内容
已知一个三角形的三边长分别是5,5,6,一只蚂蚁在其内部爬行,若不考虑蚂蚁的大小,则某时刻该蚂蚁距离三角形的三个顶点的距离均超过2的概率是( )
A、1-
| ||
B、1-
| ||
C、1-
| ||
D、1-
|
考点:几何概型
专题:概率与统计
分析:分别求出该蚂蚁距离三角形的三个顶点的距离均超过2的对应事件的面积,利用几何概型的概率公式即可得到结论.
解答:
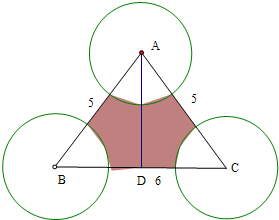 解:∵三角形的三边长分别是5,5,6,
解:∵三角形的三边长分别是5,5,6,
∴三角形的高AD=4,
则三角形ABC的面积S=
×6×4=12,
则该蚂蚁距离三角形的三个顶点的距离均超过2,对应的区域为图中阴影部分,
三个小扇形的面积之和为一个整圆的面积的
,圆的半径为2,
则阴影部分的面积为S1=12-
×π×22=12-2π,
则根据几何概型的概率公式可得所求是概率为
=1-
,
故选:C.
 解:∵三角形的三边长分别是5,5,6,
解:∵三角形的三边长分别是5,5,6,∴三角形的高AD=4,
则三角形ABC的面积S=
| 1 |
| 2 |
则该蚂蚁距离三角形的三个顶点的距离均超过2,对应的区域为图中阴影部分,
三个小扇形的面积之和为一个整圆的面积的
| 1 |
| 2 |
则阴影部分的面积为S1=12-
| 1 |
| 2 |
则根据几何概型的概率公式可得所求是概率为
| 12-2π |
| 12 |
| π |
| 6 |
故选:C.
点评:本题主要考查几何概型的概率计算,根据条件求出相应的面积是解决本题的关键,考查转化思想以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={x|(x+1)(x-2)≥0},则∁RA=( )
| A、{x|x<-1,或x>2} |
| B、{x|x≤-1,或x≥2} |
| C、{x|-1<x<2} |
| D、{x|-1≤x≤2} |
某仓库失窃,四个保管员因涉嫌而被传讯,四人供述如下
甲:我们四人都没有作案;
乙:我们四人有人作案;
丙:乙和丁至少有一个人没作案;
丁:我没有作案.
如果四人中有两个人说的是真话,有两人说的是假话,则以下断定成立的是( )
甲:我们四人都没有作案;
乙:我们四人有人作案;
丙:乙和丁至少有一个人没作案;
丁:我没有作案.
如果四人中有两个人说的是真话,有两人说的是假话,则以下断定成立的是( )
| A、说真话的是甲和丁 |
| B、说真话的是乙和丙 |
| C、说真话的是甲和丙 |
| D、说真话的是乙和丁 |
某程序框图如图所示,若该程序运行后输出的值是
,则( )

| 7 |
| 4 |

| A、a=3 | B、a=4 |
| C、a=5 | D、a=6 |

 某校男女篮球队各有10名队员,现将这20名队员的身高绘制成如图所示茎叶图(单位:cm).男队员身高在180cm以上定义为“高个子”,女队员身高在170cm以上定义为“高个子”,其他队员定义为“非高个子”.用分层抽样的方法,从“高个子”和“非高个子”中共抽取5名队员.
某校男女篮球队各有10名队员,现将这20名队员的身高绘制成如图所示茎叶图(单位:cm).男队员身高在180cm以上定义为“高个子”,女队员身高在170cm以上定义为“高个子”,其他队员定义为“非高个子”.用分层抽样的方法,从“高个子”和“非高个子”中共抽取5名队员.