题目内容
已知函数f(x)=xlnx,
(Ⅰ)求函数f(x)在[1,3]上的最小值;
(Ⅱ)若存在x∈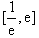 (e为自然对数的底数,且e=2.71828…)使不等式2 f(x)≥-x2+ax-3成立,求实数a的取值范围。
(e为自然对数的底数,且e=2.71828…)使不等式2 f(x)≥-x2+ax-3成立,求实数a的取值范围。
(Ⅰ)求函数f(x)在[1,3]上的最小值;
(Ⅱ)若存在x∈
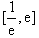 (e为自然对数的底数,且e=2.71828…)使不等式2 f(x)≥-x2+ax-3成立,求实数a的取值范围。
(e为自然对数的底数,且e=2.71828…)使不等式2 f(x)≥-x2+ax-3成立,求实数a的取值范围。 解:(Ⅰ)由 ,
,
当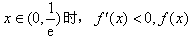 单调递减;
单调递减;
当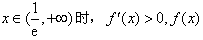 单调递增,
单调递增,
所以函数f(x)在[1,3]上单调递增,
又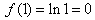 ,
,
所以函数f(x)在[1,3]上的最小值为0。
(Ⅱ)由题意知,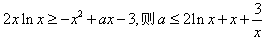 ,
,
若存在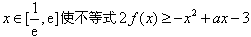 成立,
成立,
只需a小于或等于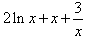 的最大值,
的最大值,
设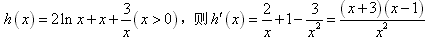 ,
,
当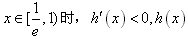 单调递减;
单调递减;
当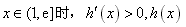 单调递增,
单调递增,
由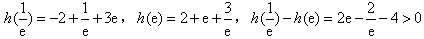 ,
,
可得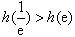 ,
,
所以,当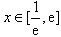 时,h(x)的最大值为
时,h(x)的最大值为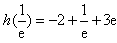 ,
,
故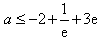 。
。
 ,
,当
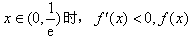 单调递减;
单调递减;当
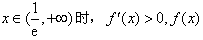 单调递增,
单调递增,所以函数f(x)在[1,3]上单调递增,
又
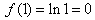 ,
,所以函数f(x)在[1,3]上的最小值为0。
(Ⅱ)由题意知,
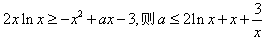 ,
,若存在
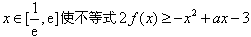 成立,
成立,只需a小于或等于
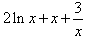 的最大值,
的最大值,设
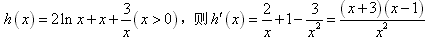 ,
,当
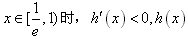 单调递减;
单调递减;当
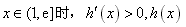 单调递增,
单调递增,由
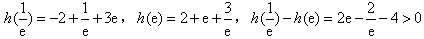 ,
,可得
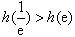 ,
,所以,当
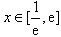 时,h(x)的最大值为
时,h(x)的最大值为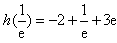 ,
,故
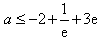 。
。 
练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|