题目内容
设函数f(x)=log2(
)(a∈R),若f(-
)=-1.
(1)求f(x)解析式并判断其奇偶性;
(2)当x∈[-1,0)时,求f(3x)的值域;
(3)g(x)=log
,若x∈[
,
]时,f(x)≤g(x)有解,求实数k取值集合.
| 1+x |
| 1-ax |
| 1 |
| 3 |
(1)求f(x)解析式并判断其奇偶性;
(2)当x∈[-1,0)时,求f(3x)的值域;
(3)g(x)=log
| 2 |
| 1+x |
| k |
| 1 |
| 2 |
| 2 |
| 3 |
(1)由于f(-
)=log2
=-1,∴
=
,即
=1+
,解得a=1,
∴f(x)=log2
.
再由
>0,求得-1<x<1
,∴定义域为(-1,1),定义域关于原点对称.
再根据f(-x)=log2
=log2(
)-1=-log2
=-f(x)
∴f(x)为奇函数.-----(3分)
(2)f(x)=log2(-1-
),∴f(3x)=log2(-1-
).
∵-1≤x<0,∴-
≤3x-1<0,∴
≤-3,即-
≥3,
∴-1-
≥2,∴log2(-1-
)≥log22=1,
∴值域为[1,+∞).-----(7分)
(3)∵log2
≤log
=2log2
=log2(
)2,∴
≤(
)2.
∵
≤x≤
,∴x+1>0.-------(9分)
令 h(x)=1-x2,显然h(x)在[
,
]上是减函数,∴h(x)max=h(
)=
,
∴只需k2≤
.又由g(x)定义域知k>0,∴0<k≤
,即k的范围为 (0,
).-----(13分)
| 1 |
| 3 |
1-
| ||
1+
|
| ||
1+
|
| 1 |
| 2 |
| 4 |
| 3 |
| a |
| 3 |
∴f(x)=log2
| 1+x |
| 1-x |
再由
| 1+x |
| 1-x |
,∴定义域为(-1,1),定义域关于原点对称.
再根据f(-x)=log2
| 1-x |
| 1+x |
| 1+x |
| 1-x |
| 1+x |
| 1-x |
∴f(x)为奇函数.-----(3分)
(2)f(x)=log2(-1-
| 2 |
| x-1 |
| 2 |
| 3x-1 |
∵-1≤x<0,∴-
| 2 |
| 3 |
| 2 |
| 3x-1 |
| 2 |
| 3x-1 |
∴-1-
| 2 |
| 3x-1 |
| 2 |
| 3x-1 |
∴值域为[1,+∞).-----(7分)
(3)∵log2
| 1+x |
| 1-x |
| 2 |
| 1+x |
| k |
| 1+x |
| k |
| 1+x |
| k |
| 1+x |
| 1-x |
| 1+x |
| k |
∵
| 1 |
| 2 |
| 2 |
| 3 |
令 h(x)=1-x2,显然h(x)在[
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
∴只需k2≤
| 3 |
| 4 |
| ||
| 2 |
| ||
| 2 |

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
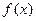 的定义域为R,若
的定义域为R,若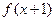 与
与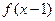 都是奇函数,则( )
都是奇函数,则( ) 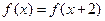
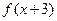 是奇函数
是奇函数