题目内容
已知{an}是等比数列，Sn是它的前n项和且Sn+an=4.(1)求an和Sn；
(2)是否存在正整数c和k，使得
＞2成立.
解：(1)Sn+an=4，令n=1,2得
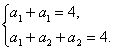
∴a1=2,a2=1,∴q=
,
∴an=2·(
)n-1=(
)n-2,
Sn=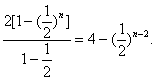
(2)假设存在正整数c、k使不等式成立，即：
＜4-c＜3·
2＜(4-c)·
＜3.
∵c、k是正整数，
∴(4-c)·
是整数，与上式矛盾，故不存在正整数c、k使不等式成立.
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目