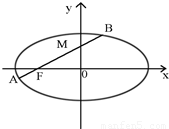
题目内容
 过椭圆
过椭圆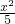 +
+ =1的左焦点F作椭圆的弦AB.如图
=1的左焦点F作椭圆的弦AB.如图
(1)求此椭圆的左焦点F的坐标和椭圆的准线方程(x=± );
);
(2)求弦AB中点M的轨迹方程.
 解:(1)由方程知 a=
解:(1)由方程知 a= ,b=2,故左焦点F(-1,0),
,b=2,故左焦点F(-1,0),离心率 e=
 =
= .
.(2)设M(x,y),A( x1,y1 ),B(x2,y2 ),直线AB方程为 y=k(x+1),
由
 消y得:(4+5k2)x2+10k2 x+5k-20=0,
消y得:(4+5k2)x2+10k2 x+5k-20=0,∴x1+x2=
 ,因为M是AB中点,有 x=
,因为M是AB中点,有 x= ,
,∴x=
 ,∴k2=
,∴k2= ,
,又由 y=k(x+1)可得 y2=k2(x+1)2,∴y2=
 (x+1)2,
(x+1)2,∴5y2=-4x(x+1),即 4x2+4x+5y2=0,即 4
 +5y2=1,
+5y2=1,当直线AB的斜率k不存在时,AB⊥x轴,AB中点M 的坐标为(-1,0),也适合上述方程,
故 4
 +5y2=1 为所求.
+5y2=1 为所求.分析:(1)由方程知 a=
 ,b=2,从而求得焦点坐标和离心率的值.
,b=2,从而求得焦点坐标和离心率的值.(2)由
 消y得:(4+5k2)x2+10k2 x+5k-20=0,故 x1+x2=
消y得:(4+5k2)x2+10k2 x+5k-20=0,故 x1+x2= ,再由中点公式得x=
,再由中点公式得x= ,又由 y=k(x+1)可得 4x2+4x+5y2=0,即为所求.
,又由 y=k(x+1)可得 4x2+4x+5y2=0,即为所求.点评:本题考查点轨迹方程的求法,椭圆的简单性质的应用,体现了分类讨论的数学思想,得到 y2=
 (x+1)2,是解题的关键.
(x+1)2,是解题的关键. 
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 +
+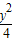 =1的左焦点F作椭圆的弦AB.如图
=1的左焦点F作椭圆的弦AB.如图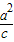 );
);