题目内容
如果学生甲每次投篮投中的概率为| 1 | 3 |
分析:(1)由题意知,它是一个二项分布,利用二项分布的概率公式;
(2)题目中:“至少有一次投中”,包含诸多情形,不如考虑它的对立事件“一次都没投中”.先计算它的概率值,后即可得至少有一次投中的概率.
(2)题目中:“至少有一次投中”,包含诸多情形,不如考虑它的对立事件“一次都没投中”.先计算它的概率值,后即可得至少有一次投中的概率.
解答:解:①C32(
)2(
)=
,
②“至少有一次投中”的对立事件是“一次都没投中”.
“一次都没投中”的概率为
=(
)3=
,故“至少有一次投中”的概率为P=1-
=1-
=
.
故填:
,
.
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
②“至少有一次投中”的对立事件是“一次都没投中”.
“一次都没投中”的概率为
| P |
| 2 |
| 3 |
| 8 |
| 27 |
| P |
| 8 |
| 27 |
| 19 |
| 27 |
故填:
| 2 |
| 9 |
| 19 |
| 27 |
点评:本题考查了对立事件的概率这个知识点.本题易错点:不会运用对立事件的概率,计算繁琐,导致耗时易错.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 次,每次投篮的结果相互独立.在
次,每次投篮的结果相互独立.在 处每投进一球得
处每投进一球得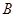 处每投进一球得
处每投进一球得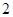 分,否则得
分,否则得 分. 将学生得分逐次累加并用
分. 将学生得分逐次累加并用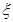 表示,如果
表示,如果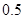 ,在
,在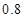 .
.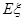 ;
; ,那么他连续投三次,恰好两次投中的概率为 ;至少有一次投中的概率为 (用数字作答).
,那么他连续投三次,恰好两次投中的概率为 ;至少有一次投中的概率为 (用数字作答).