题目内容
15.从3名男同学,n名女同学中任选2名参加英语口语比赛,其中至少有1名女同学的概率为$\frac{25}{28}$,则女生人数为5人.分析 利用组合数公式求出至少有1名女同学参加的基本事件个数和基本事件的总个数,利用概率公式列方程解出.
解答 解:设女生由n人,则共有n+3名同学.
从这n+3名同学中任选2人的基本事件个数为${C}_{n+3}^{2}$=$\frac{(n+3)(n+2)}{2}$,
其中至少有1名女生的基本事件为${C}_{3}^{1}$${C}_{n}^{1}$+${C}_{n}^{2}$=3n+$\frac{n(n-1)}{2}$.
∴其中至少有1名女同学的概率为$\frac{\frac{{n}^{2}+5n}{2}}{\frac{{n}^{2}+5n+6}{2}}$=$\frac{{n}^{2}+5n}{{n}^{2}+5n+6}=\frac{25}{28}$.
解得n=5.
故答案为5.
点评 本题考查了古典概型的概率计算,组合数公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.执行如图所示的程序框图,若输出s的值为11,那么输入的n值等于( )


| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
3.“-$\frac{1}{2}<x<1$”是“不等式|x-1|<1成立”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分亦非必要条件 |
10.设A={1,2,(m2-3m+1)+(m2-5m-6)i},B={-1,5},A∩B={5},则实数m的值为( )
| A. | -1 | B. | -4 | C. | -1或4 | D. | 1或-4 |
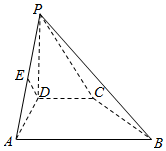 如图,在四棱锥P-ABCD中,PD⊥面ABCD,AB∥DC,AB⊥AD,DC=6,AD=8,BC=10,∠PAD=45°,E为PA的中点.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AB∥DC,AB⊥AD,DC=6,AD=8,BC=10,∠PAD=45°,E为PA的中点.