Question

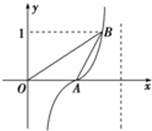函数y=tan（

π

4

x-

π

2

）的部分图象如图所示，则（O

B

-

OA

）•

OB

=

 

．

Answer 1

分析：令y=tan(

π

4

x-

π

2

)=0，则

π

4

x-

π

2

=kπ（k∈Z），取k=0，即可得到点A的坐标．令y=tan(

π

4

x-

π

2

)=1，则

π

4

x-

π

2

=kπ+

π

4

（k∈Z），取k=0，即可得到点B的坐标．再利用数量积运算即可得出．

解答：解：令y=tan(

π

4

x-

π

2

)=0，则

π

4

x-

π

2

=kπ（k∈Z），
取k=0，解得x=2，∴A（2，0）．
令y=tan(

π

4

x-

π

2

)=1，则

π

4

x-

π

2

=kπ+

π

4

（k∈Z），
取k=0，解得x=3，∴B（3，1）．
∴（

OB

-

OA

）•

OB

=[（3，1）-（2，0）]•（3，1）=4．
故答案为：4．

点评：本题考查了正切函数的图象与性质、数量积运算，属于中档题．