题目内容
设命题p:
(x,y,k∈R,且k>0)命题q:(x-3)2+y2≤25(x,y∈R),若P是q的充分不必要条件,则k的取值范围是( )
|
分析:已知命题p:
命题q:(x-3)2+y2≤25(x,y∈R),p是q的充分不必要条件可得p⇒q,说明p所表示的区域在q所表示的区域内部,画出p和q的可行域,利用数形结合的方法进行求解;
|
解答:解:由题意可得,p是q的充分不必要条件,可得p⇒q,
说明p所表示的区域在q所表示的区域内部,数形结合,画出p和q的区域范围,
如下图:

B(k,4-
k),
可知只需满足条件:
∴
,解得0<k≤6;
故选B;
说明p所表示的区域在q所表示的区域内部,数形结合,画出p和q的区域范围,
如下图:

B(k,4-
| 4 |
| 3 |
可知只需满足条件:
|
∴
|
故选B;
点评:此题主要考查线性规划问题,解题的过程中用到了数形结合的方法,解决此题的关键是能够正确画出可行域,此题是一道中档题;

练习册系列答案
相关题目
 ,
, 均为单位向量,若|
均为单位向量,若|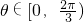
 ],且|x1|>|x2|时,有f(x1)>f(x2),
],且|x1|>|x2|时,有f(x1)>f(x2), ,
, 均为单位向量,若|
均为单位向量,若| +
+ |>1,则
|>1,则
 ],且|x1|>|x2|时,有f(x1)>f(x2),
],且|x1|>|x2|时,有f(x1)>f(x2),