题目内容
设A={x|x=kπ+ ,k∈Z },已知
,k∈Z },已知 =( 2cos
=( 2cos ,sin
,sin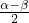 ),
), =(cos
=(cos ,3sin
,3sin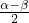 ),
),
(1)若α+β= ,且
,且 =2
=2 ,求α,β的值.
,求α,β的值.
(2)若 =
= ,其中 α,β∈A,求tanαtanβ的值.
,其中 α,β∈A,求tanαtanβ的值.
解:(1)∵α+β= ,
,
∴ =(1,sin(
=(1,sin(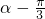 )),
)), =(
=( ,3sin(
,3sin(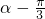 )),(4分)
)),(4分)
由 =2
=2 ,,得sin(
,,得sin(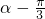 )=0,
)=0,
∴α=kπ+ ,β=-kπ+
,β=-kπ+ ,k∈Z.(3分)
,k∈Z.(3分)
(2)∵ =2cos2
=2cos2 +3sin2
+3sin2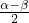
=1+cos(α+β)+3×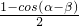
= +cos(α+β)-
+cos(α+β)- cos(α-β)=
cos(α-β)= ,(3分)
,(3分)
∴cos(α+β)= cos(α-β),
cos(α-β),
展开得2cosα•cosβ-2sinα•sinβ=3cosα•cosβ+3sinα•sinβ
即-5sinα•sinβ=cosα•cosβ,
∵α,β∈A,
∴tanα•tanβ=- .(4分)
.(4分)
分析:(1)由α+β= ,我们易将向量
,我们易将向量 ,
, 化为
化为 =(1,sin(
=(1,sin(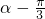 )),
)), =(
=( ,3sin(
,3sin(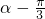 ))的形式,结合
))的形式,结合 =2
=2 ,我们构造三角方程,解方程即可求出满足条件的α,β的值.
,我们构造三角方程,解方程即可求出满足条件的α,β的值.
(2)由已知中 =( 2cos
=( 2cos ,sin
,sin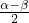 ),
), =(cos
=(cos ,3sin
,3sin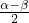 ),及
),及 =
= ,我们易构造一个关于α,β的关系式,结合两角和与差的余弦公式,我们易求出
,我们易构造一个关于α,β的关系式,结合两角和与差的余弦公式,我们易求出
-5sinα•sinβ=cosα•cosβ,进而得到答案.
点评:本题考查的知识点是同角三角函数的基本关系,向量加法及其几何意义,平面向量数量积的运算,熟练掌握三角函数公式及向量数量积的定义,是解答本题的关键.
 ,
,∴
 =(1,sin(
=(1,sin(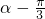 )),
)), =(
=( ,3sin(
,3sin(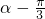 )),(4分)
)),(4分)由
 =2
=2 ,,得sin(
,,得sin(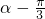 )=0,
)=0,∴α=kπ+
 ,β=-kπ+
,β=-kπ+ ,k∈Z.(3分)
,k∈Z.(3分)(2)∵
 =2cos2
=2cos2 +3sin2
+3sin2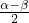
=1+cos(α+β)+3×
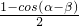
=
 +cos(α+β)-
+cos(α+β)- cos(α-β)=
cos(α-β)= ,(3分)
,(3分)∴cos(α+β)=
 cos(α-β),
cos(α-β),展开得2cosα•cosβ-2sinα•sinβ=3cosα•cosβ+3sinα•sinβ
即-5sinα•sinβ=cosα•cosβ,
∵α,β∈A,
∴tanα•tanβ=-
 .(4分)
.(4分)分析:(1)由α+β=
 ,我们易将向量
,我们易将向量 ,
, 化为
化为 =(1,sin(
=(1,sin(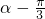 )),
)), =(
=( ,3sin(
,3sin(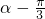 ))的形式,结合
))的形式,结合 =2
=2 ,我们构造三角方程,解方程即可求出满足条件的α,β的值.
,我们构造三角方程,解方程即可求出满足条件的α,β的值.(2)由已知中
 =( 2cos
=( 2cos ,sin
,sin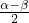 ),
), =(cos
=(cos ,3sin
,3sin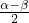 ),及
),及 =
= ,我们易构造一个关于α,β的关系式,结合两角和与差的余弦公式,我们易求出
,我们易构造一个关于α,β的关系式,结合两角和与差的余弦公式,我们易求出-5sinα•sinβ=cosα•cosβ,进而得到答案.
点评:本题考查的知识点是同角三角函数的基本关系,向量加法及其几何意义,平面向量数量积的运算,熟练掌握三角函数公式及向量数量积的定义,是解答本题的关键.

练习册系列答案
相关题目