Question

计算：(1)lg³2＋lg³5＋3lg 2·lg 5；

(2)已知log_a2＝m，log_a3＝n，求a^2m+n的值；

(3)已知10^a＝2，10^b＝3，求100^2a－b的值．

Answer 1

答案：
解析：

　　解：(1)lg³2＋lg³5＋3lg 2·lg 5

　　＝(lg 2＋lg 5)(lg²2－lg 2·lg 5＋lg²5)＋3lg 2·lg 5

　　＝lg 10[(lg 2＋lg 5)²－3lg 2·lg 5]＋3lg 2·lg 5

　　＝1．

　　∵log_a2＝m，∴a^m＝2．

　　∵log_a3＝n，∴aⁿ＝3．

　　方法1：故a^2m+n＝(a^m)²·aⁿ＝4×3＝12．

　　方法2：∵log_a2＝m，log_a3＝n，

　　

　　(3)方法1：∵10^a＝2，∴lg 2＝a．

　　∵10^b＝3，∴lg 3＝b．

　　

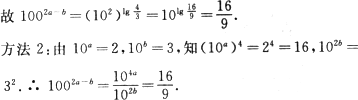
提示：

　　分析：(1)由式子结构想到立方和公式a³＋b³＝(a＋b)(a²－ab＋b²)．

　　(2)、(3)小题可以根据式子结构特征，将已知式子变式，再代入求值．

　　解题心得：(1)利用对数的运算性质计算时，常将式子化为含有lg 2＋lg 5(＝1)的式子，解题中应灵活运用有关乘法公式．

　　(2)注意解题中整体代换，如lg 2＋lg 5可用1替代等．