题目内容
7.设S表示所有大于-1的实数构成的集合,确定所有的函数:S→S,满足以下两个条件:(1)对于S内的所有x和y,f(x+f(y)+xf(y))=y+f(x)+yf(x);
(2)在区间-1<x<0与x>0的每一个内,$\frac{f(x)}{x}$是严格递增的.
求满足上述条件的函数的方程.
分析 令y=x可得f(x+f(x)+xf(x))=x+f(x)+xf(x),令x+f(x)+xf(x)=c,则f(c)=c,代入(1)可得f(2c+c2)=2c+c2.对c的符号进行讨论得出c=0即x+f(x)+xf(x)=0,从而得出f(x)的解析式.
解答 解:令y=x得f(x+f(x)+xf(x))=x+f(x)+xf(x),
令x+f(x)+xf(x)=c,则f(c)=c,
带入(1)得f(2c+c2)=2c+c2.∵2+c>2+(-1)=1,∴2c+c2=c(2+c)与c同号.
若c>0,则2c+c2>c,但$\frac{{f(2c+{c^2})}}{{2c+{c^2}}}=\frac{f(c)}{c}=1$,与$\frac{f(x)}{x}$在x>0时严格递增相矛盾,
若c<0,同样导出矛盾,
∴c=0,从而对一切x∈S有x+f(x)+xf(x)=0,
∴$f(x)=-\frac{x}{x+1}$.
点评 本题考查了抽象函数的性质的应用,属于中档题.

练习册系列答案
相关题目
18.若x,y满足$\left\{\begin{array}{l}x+y≤4\\ x-2y≥0\\ x+2y≥4\end{array}$则z=$\frac{y-4}{x}$的取值范围是( )
| A. | $(-∞,-\frac{3}{2}]∪[-1,+∞)$ | B. | $(-∞,-\frac{5}{2}]∪[-1,+∞)$ | C. | $[-\frac{5}{2},-\frac{3}{2}]$ | D. | $[-\frac{3}{2},-1]$ |
15.设函数f(x)=$\left\{\begin{array}{l}{3x-b(x<1)}\\{{3}^{x}(x≥1)}\end{array}\right.$,若$f(f(\frac{1}{2}))=9$,则实数b的值为( )
| A. | $-\frac{3}{2}$ | B. | $-\frac{9}{8}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{1}{2}$ |
2.已知α∈(-$\frac{π}{2}$,$\frac{π}{2}$),β∈($-\frac{π}{2}$,$\frac{π}{2}$),若tanα,tanβ是方程x2+4$\sqrt{3}$x+5=0的两根,则α+β=( )
| A. | $-\frac{2}{3}π$ | B. | $\frac{π}{3}$ | C. | $\frac{2}{3}π$ | D. | $-\frac{2}{3}π$或$\frac{π}{3}$ |
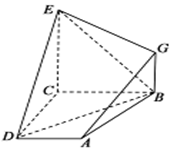 如图,已知四边形BCD和BCEG均为直角梯形,AD∥EG、CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=2AD,CE=2BG.求证:
如图,已知四边形BCD和BCEG均为直角梯形,AD∥EG、CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=2AD,CE=2BG.求证: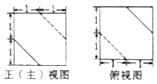 已知一个正方体截取两个全等的小正三棱锥后得到的几何体的主视图和俯视图如图,则该几何体的左视图为( )
已知一个正方体截取两个全等的小正三棱锥后得到的几何体的主视图和俯视图如图,则该几何体的左视图为( )


