题目内容
已知四边形ABCD为圆内接四边形，AB是直径，MN切⊙O于C点，∠BCM=38°，那么∠ABC的度数是52°
52°
．分析：利用MN切⊙O于C点，可得弦切角等于同弧所对的圆周角，再利用AB是直径，即可求得∠ABC的度数
解答：
解：连接AC，则∵MN切⊙O于C点
∴∠BCM=∠BAC=38°
∵AB是直径，
∴∠ABC=90°-∠BAC=90°-38°=52°
故答案为：52°
解：连接AC，则∵MN切⊙O于C点∴∠BCM=∠BAC=38°
∵AB是直径，
∴∠ABC=90°-∠BAC=90°-38°=52°
故答案为：52°
点评：本题考查弦切角定理，考查直径所对的圆周角为直角，解题的关键是利用定理正确求解．
练习册系列答案
相关题目
如图，已知四边形ABCD为矩形，AD⊥平面ABE，AE=EB=BC=2，F为CE上的点，且BF⊥平面ACE．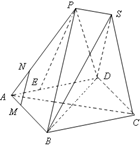
已知四边形ABCD为菱形，AB=6，∠BAD=60°，两个正三棱锥P-ABD、S-BCD（底面是正三角形且顶点在底面上的射影是底面正三角形的中心）的侧棱长都相等，如图，E、M、N分别在AD、
如图，已知四边形ABCD为直角梯形，∠ABC=90°，AD∥BC，AD=2，AB=BC=1，沿AC将△ABC折起，使点B到点P的位置，且平面PAC⊥平面ACD．
已知四边形ABCD为直角梯形，∠ADC=90°，AD∥BC，△ABD为等腰直角三角形，平面PAD⊥平面ABCD，E为PA的中点，AD=2BC=