题目内容
已知椭圆 的焦点分别是F1,F2
的焦点分别是F1,F2
(1)求椭圆的离心率e;
(2)设点P在这个椭圆上,且|PF1|-|PF2|=1,求∠F1PF2的余弦值.
解:(1)因为椭圆 ,所以a=2,b=
,所以a=2,b= ,c=1,∴
,c=1,∴ …(5分)
…(5分)
(2)由
解得 ,
,
又|F1F2|=2,
由余弦定理可得cos∠F1PF2= …(12分)
…(12分)
分析:(1)通过椭圆方程求出a,b,c,然后求椭圆的离心率e;
(2)通过椭圆的定义以及|PF1|-|PF2|=1,利用余弦定理直接求∠F1PF2的余弦值.
点评:本题考查椭圆的简单性质,椭圆的定义以及余弦定理的应用,考查计算能力.
 ,所以a=2,b=
,所以a=2,b= ,c=1,∴
,c=1,∴ …(5分)
…(5分)(2)由

解得
 ,
,
又|F1F2|=2,
由余弦定理可得cos∠F1PF2=
 …(12分)
…(12分)分析:(1)通过椭圆方程求出a,b,c,然后求椭圆的离心率e;
(2)通过椭圆的定义以及|PF1|-|PF2|=1,利用余弦定理直接求∠F1PF2的余弦值.
点评:本题考查椭圆的简单性质,椭圆的定义以及余弦定理的应用,考查计算能力.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 的焦点分别是
的焦点分别是
 ;
; -
-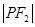 =1,求
=1,求 的余弦值.
的余弦值.